Introduction
전자기기의 발전에 따라, 웨어러블 디바이스의 개념이 달라지며 발전이 이루어졌다. 기존에는 시계로 대표되는 웨어러블 디바이스였는데, 이 시계가 전자기기로 변경되면서, 웨어러블 디바이스에서의 중요성이 경량화, 착용감, 안정성 등이 추가되었다.
실제 웨어러블 디바이스의 밴드는 기존의 천이나 가죽, 메탈 등의 소재에서, 고분자 소재로 변경되고 있으며, 이러한 고분자 소재는 성형이 쉽고, 가격이 낮으며 디자인과 색상에서의 강점이 있다. 또한 천/가죽 등의 천연 소재보다 내구성이 높고 소재에 따라 다르겠지만 메탈 대비 착용감이 좋다는 점도 있다. 이러한 고분자 소재 기반 웨어러블 디바이스의 제작은 자동 제어화가 가능하여 인력의 낭비가 적으며, 복잡한 모양이나 어려운 구조도 금형 설계를 통해 높은 정밀도로 표현 해 낼 수 있다.1-3
이러한 웨어러블 디바이스 밴드용 고분자 재료의 제품 대부분은 아주 단순한 구조4로 이루어져 있는데, 최근에는 특수한 디자인의 제품들이 출시되고 있다. 이러한 특수한 디자인의 제품의 경우에는 내구성이나 구조적 취약점5,6이 발생할 수 있으며, 실제 제품 적용까지 내구성 테스트를 진행하여야 하고 이는 디자인 개발에 있어 시간을 많이 소요시키는 원인7 중 하나로 볼 수 있다.
고분자 재료 중 웨어러블 디바이스에는 주로 고분자 엘라스토머 복합재(TPE)가 재료로 사용 되는데, 이러한 TPE는 고무와 플라스틱의 성질을 모두 가지고 있어, 우리가 원하는 경량화 및 착용감, 안정성에서의 강점을 가지고 있다.8 이러한 고분자 엘라스토머 복합재 중에는 합성 기반에 따라 여러가지로 나뉠 수 있는데, 이 중 화학적 안정성이 높고 성형이 용이한 TPE를 웨어러블 디바이스용 밴드에 적용하는 경우9가 많아, 이를 해석하여 적용하는 연구가 필요하다.
본 연구에서는 다양한 디자인을 통해 변경된 구조에 대해 초탄성(hyperelastic)해석 모델 중 두 가지 해석 모델 및 선형(Linear) 해석 모델을 적용하여 변형 상태에서의 물성 변화를 관찰하였다. 이를 통해 디자인에 따른 취약점에 대한 데이터를 확보하여 실제 상황에 응용하고자 한다.
Material Information
본 해석 및 실험에 사용한 재료는 삼양사에서 제조한 TPE (TPC-ET)를 사용하였으며, Figure 1에 그 구조와 결정화 정도를 모식 하였다. 실제 TPE는 soft segment와 hard segment 가 혼합되어 있는 블락코폴리머 중합체로, 삼양사 제조 TPE의 경우에는 Hard segment로 PBT를 이용하여 PBT-Elastomer라고도 불린다. 이러한 이유로 TRIEL의 경우 결정성 분자의 거동이 PBT와 유사함을 알 수 있다.
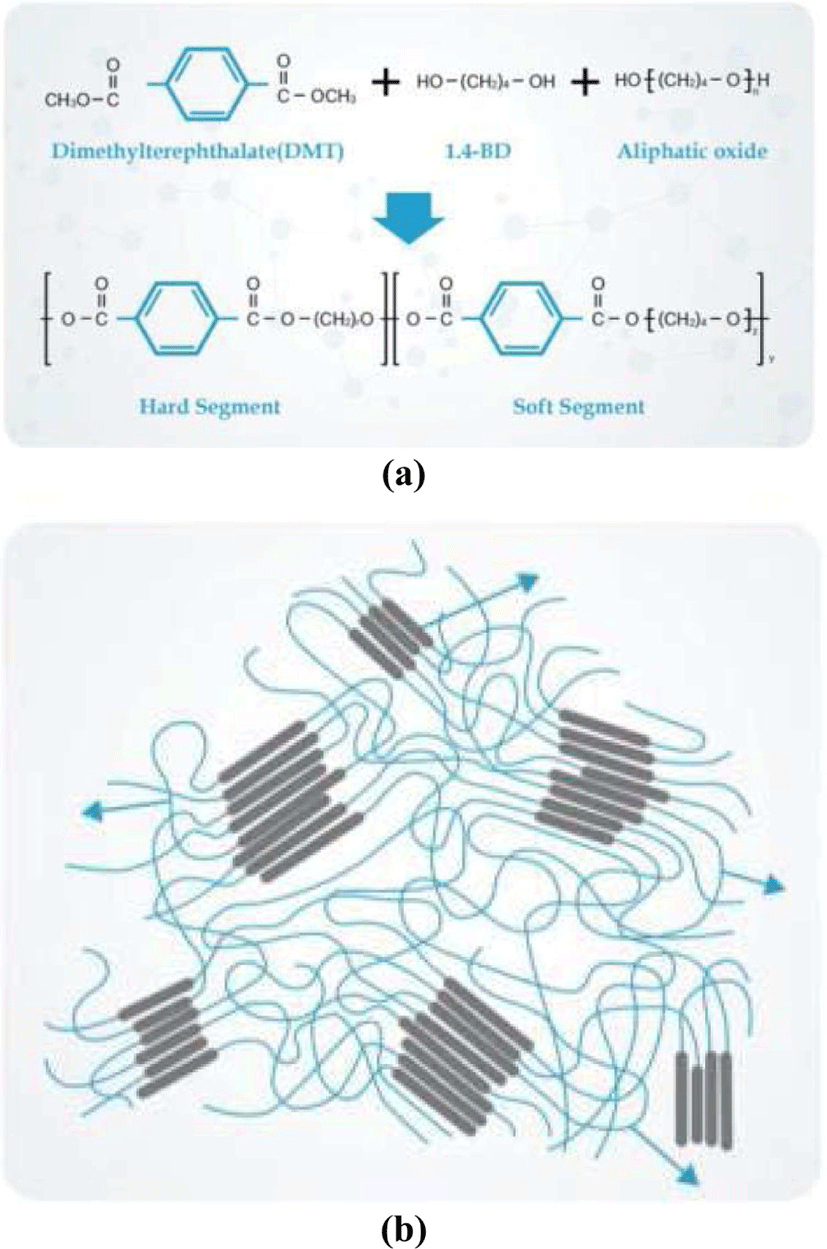
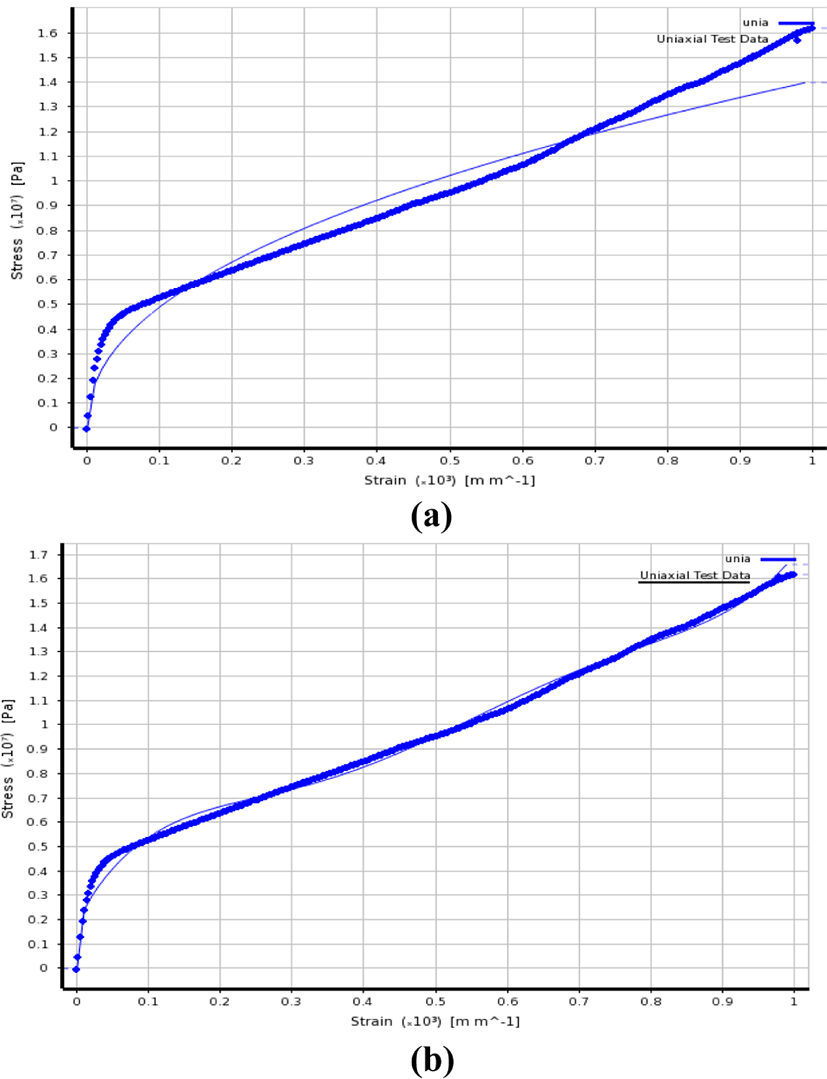
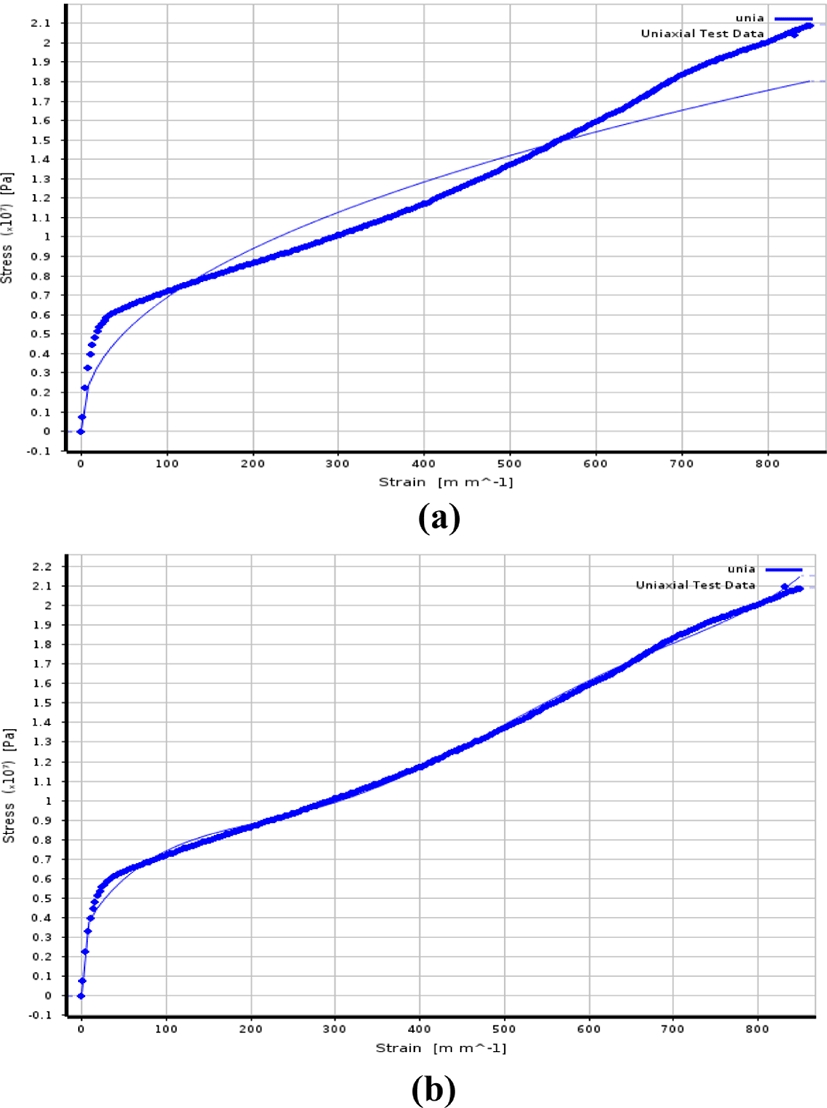
Figure 2에 해석을 위해 본 연구에서 사용한 소재의 인장-변형 곡선을 나타내었다. 경도에 따라 구분된 그레이드에 따라 인장-변형 곡선의 차이를 보이는데, 비슷한 거동을 보이는 두 가지 재료를 해석에 이용하고자 하였다. 이에 따라 본 해석에 사용한 소재는 두 가지로, TRIEL 5300NA, TRIEL 5550NA (SAMYANG)을 사용하였다.
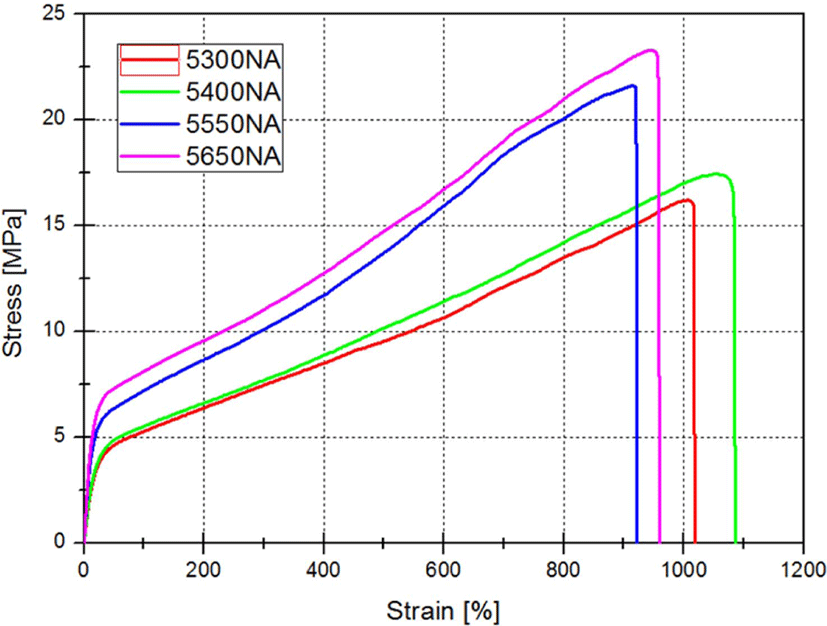
각 소재는 Shore D 경도에 따라 구분되며, 이는 Table 1에 비교하여 표기하였다.
| Item | Shore D hardness |
|---|---|
| TRIEL 5300NA | 30D |
| TRIEL 5400NA | 40D |
| TRIEL 5550NA | 55D |
| TRIEL 5650NA | 65D |
Simulation
엘라스토머 고분자의 구조해석을 진행하기 위해, 사용하는 구성 방정식에는 여러 가지가 있을 수 있다.10 본 연구에서는 ANSYS를 이용해서 구조해석을 진행하였으며, 두 가지의 초탄성 모델, 그리고 선형해석 모델을 비교하였다.
엘라스토머의 선형 해석 모델은 실제 다음과 같은 경우에 사용할 수 있다.11
-
물질의 strain이 매우 작을 때(linear)
-
Stress-strain의 비례관계가 있을 때(linear)
-
힘을 가했을 때와 힘을 놓았을 때 변형 곡선 상에서 움직여야 함(elasticity)
-
가하는 힘과 관계 없이 변형이 일어남
실제 위와 같은 경우는 고무계열 재료에서도 극 초반의 변형(S-S curve 상의 초반)에서 확인할 수 있으며, 실제 본 연구에서도 재료의 인장 시험 결과의 초반 결과를 이용할 plot을 진행하였다.
본 연구에서 사용한 두 가지 초탄성 해석 모델은 Mooney-Rivlin model과 Ogden12-15모델로, 각각은 아래와 같이 표현할 수 있다.
Meloney Mooney와 Ronald Rivlin이 소개한 Mooney-Rivlin 모델은 초탄성 해석 모델로 strain energy potential 은 아래와 같은 함수로 표현된다:
여기서 U: 단위 체적 당 strain energy, C10, C01and D1: 온도에 따른 material 고유 parameter이며, J el: 탄성 부피 계수이다.16
I1 and I2 는 Cauchy-Green deformation tensor에서의 제1, 제2 편향 요소이다.
Ogden 모델은 고무 또는 고분자 복합재와 같은 재료의 비선형 인장-변형 거동을 예측하는 데 사용할 수 있는 초탄성 모델이다.17 Ogden 모델의 strain energy potential은 아래와 같은 함수로 표현된다:
마찬가지로 U: 단위 체적 당 strain energy 이며, λi: 는 이론적인 stretches를 나타낸다.18
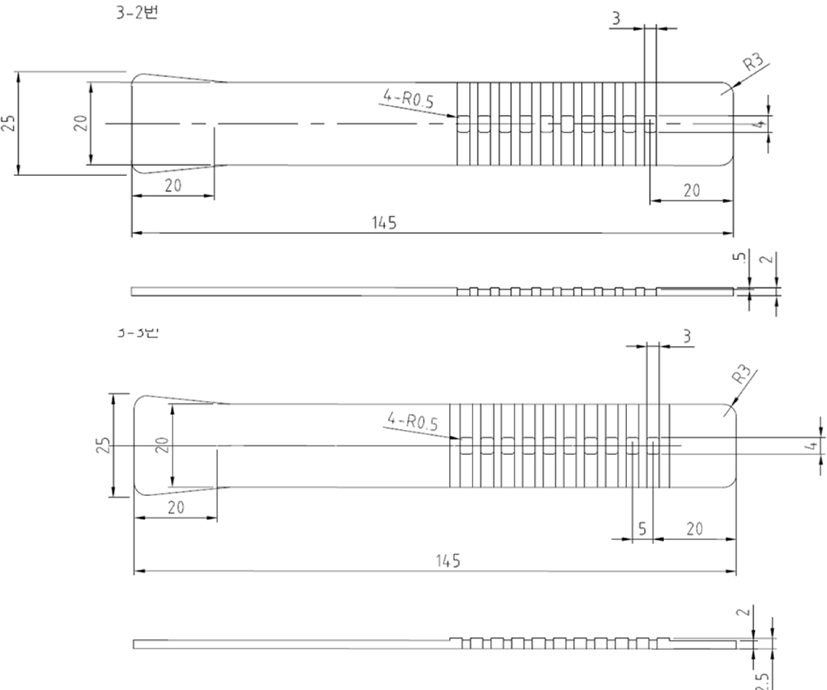
Figure 3과 Figure 4에서 해석을 위한 본 연구에서 사용한 모델의 형상과 메시(mesh)형상을 나타내었다. 첫 번째 모델은 기본적인 웨어러블 밴드 모형을 기반으로 하였으며, 두 번째와 세 번째 모델은 이 첫 번째 모델을 기반으로 하여 내부에 체결용 구멍을 뚫어 구조의 복잡성을 더했다. 이 중 두 번째 모델은 내부의 원형 구멍을 10개 내었으며, 세 번째 모델은 사각형의 구멍을 10개 내었다. 각각의 구멍의 위치는 양 끝 단으로부터 동일하며, R값 및 φ 값을 일치시킬 수 있도록 하였다. 이를 제외하면 모델의 모든 수치는 일치하여 비교 대상에서 배제할 수 있도록 하였다.
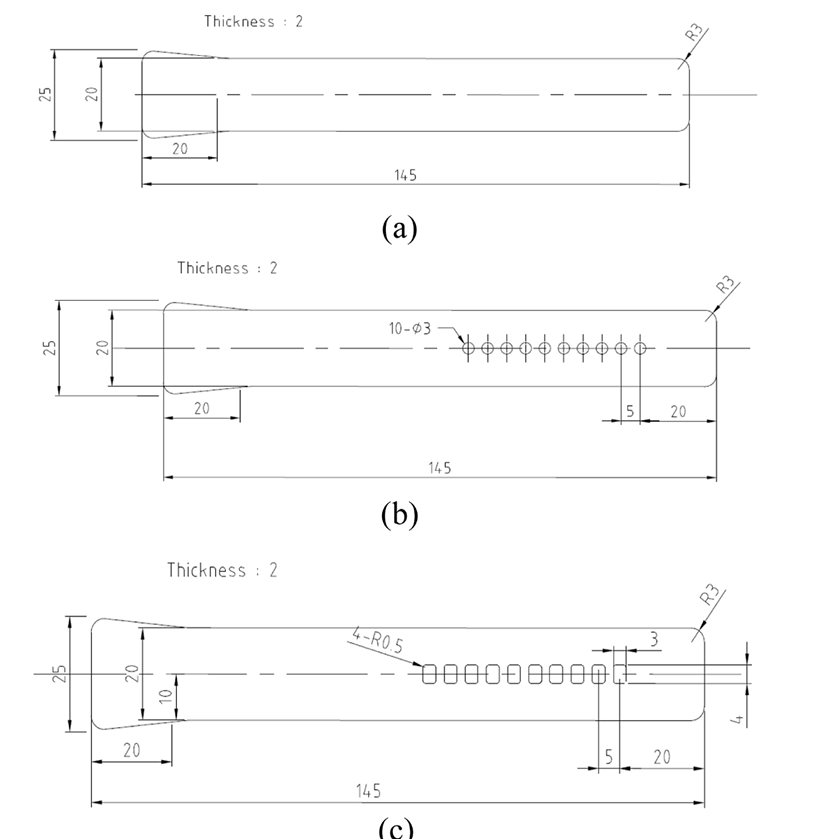
또한 추가 해석으로 진행하였던 세 번째 모델의 개량형 도안을 Figure 5에 나타내었다. 사각형 구멍을 지닌 모델의 구멍 주변에 구조적 안정감을 주기 위하여 양각 및 음각 처리를 진행하였으며, 각 양각 및 음각의 두께는 0.5 mm로 동일하게 진행하였다.
각각의 시편은 ANSYS tool을 이용한 dual domain mesh로 작업 하였으며, model 1의 경우 총 요소(element)수는 6,669개, model 2의 총 요소는 19,659 개, model 3의 총 요소는 7,640 개 이다.
본 연구에서 사용한 해석 조건은 동일하다. Figure 6에서 처럼 웨어러블 밴드의 한쪽 끝 단을 고정 면으로 하여 고정시키고, 반대편 끝 단에서의 변형을 주어 밴드의 변형 량 및 에너지 변화를 파악하고자 하였다. 변형 량은 3 mm와 10 mm로 진행하였으며, 각각의 모델을 이용하여 해석을 진행하 였다.
초탄성 모델을 이용하기 위해, ANSYS프로그램을 통해 curve fitting을 진행하였으며 그 결과는 Figure 7, 8에 표기하였다.
Results and Discussion
Figure 9에서부터 13까지 해석 결과를 보여주고 있다.
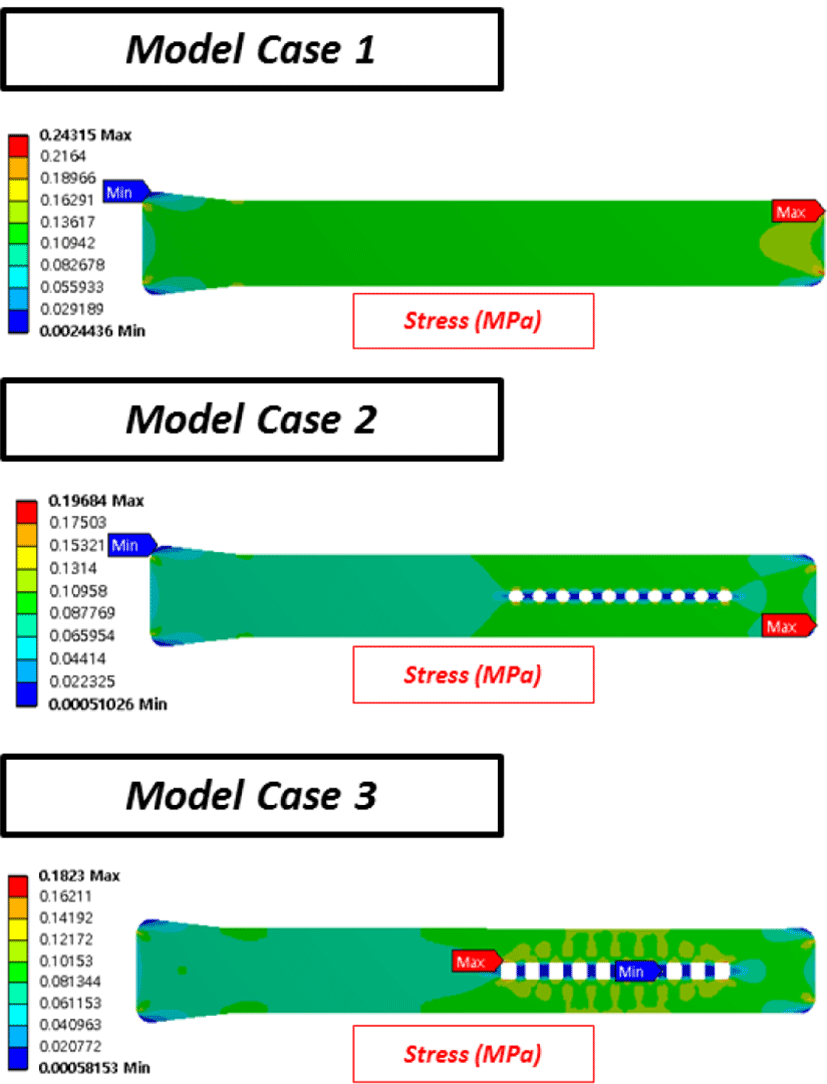
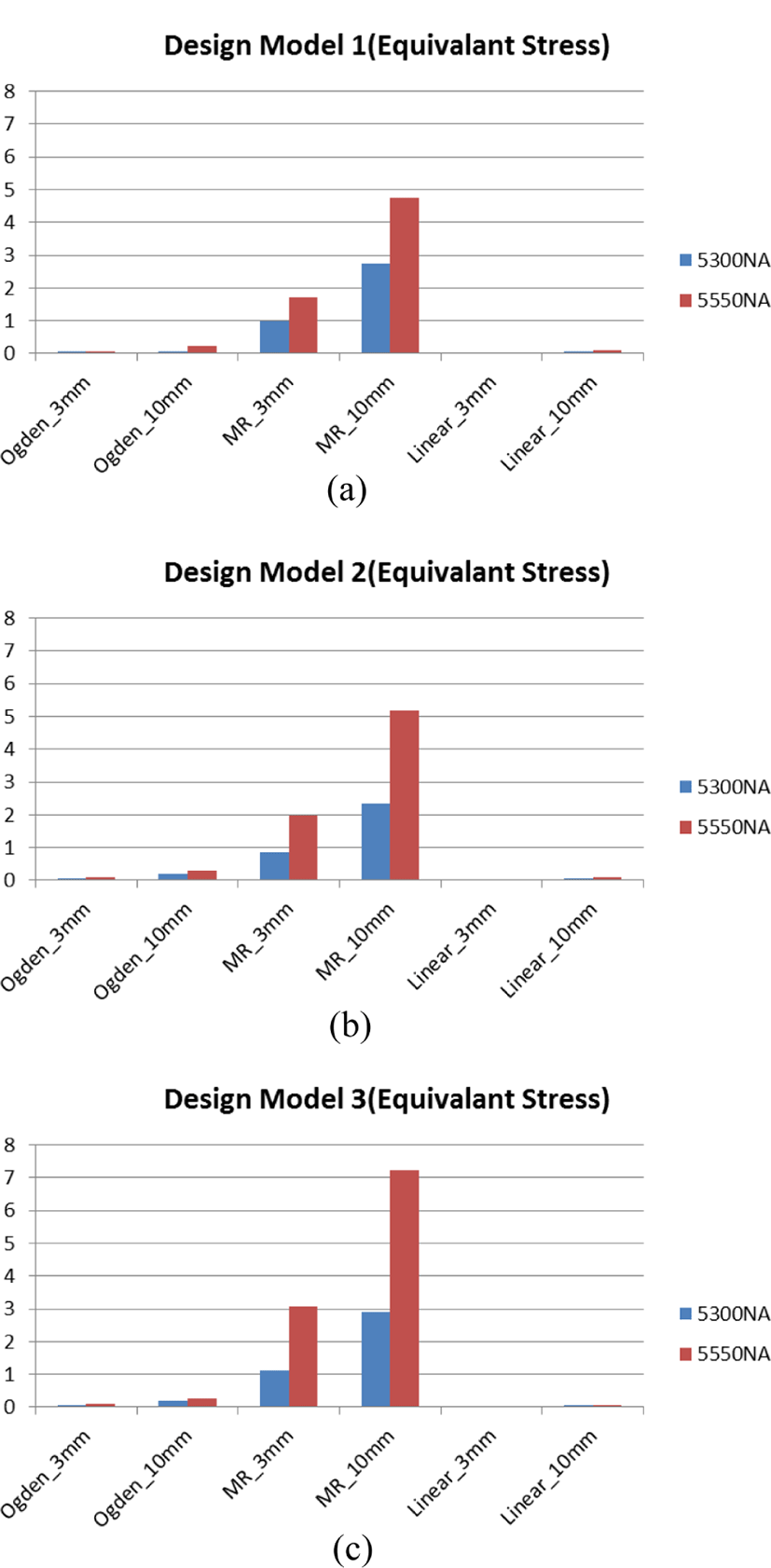
Figure 9에서 Ogden model을 이용한 각 디자인 모델 별 등가응력(equivalent stress)의 변화를 표기하였다. 모델에 따라 등가응력의 변화가 나타나며, 모델 내부의 구멍(hole) 유무에 따라 최대값의 등가응력이 나타나는 부위가 달라지는 것을 확인하였다.
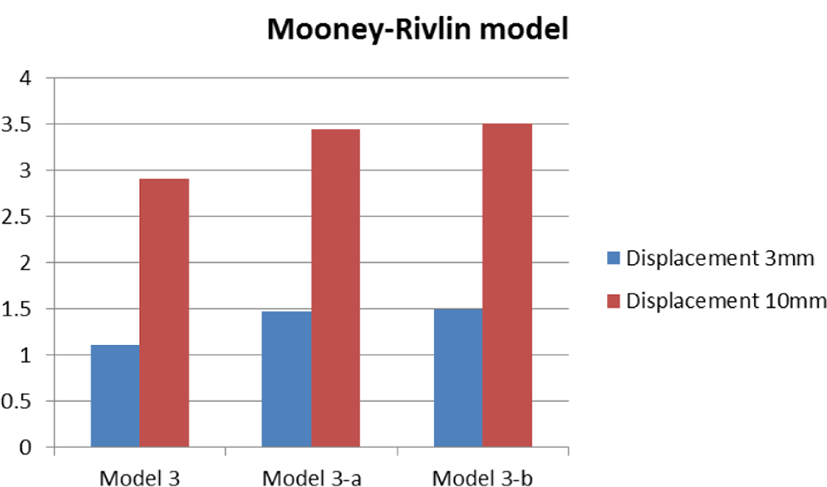
Figure 10에서는 Ogden model, Mooney-Rivlin model 및 선형탄성 모델에서의 등가응력의 변화를 표기하였다. Material 모델에 따라 등가응력 값의 변화가 나타나는데, Ogden 및 선형탄성 모델에 비해 Mooney-Rivlin 모델에서의 등가응력 값의 편차가 큰 것을 확인할 수 있다.
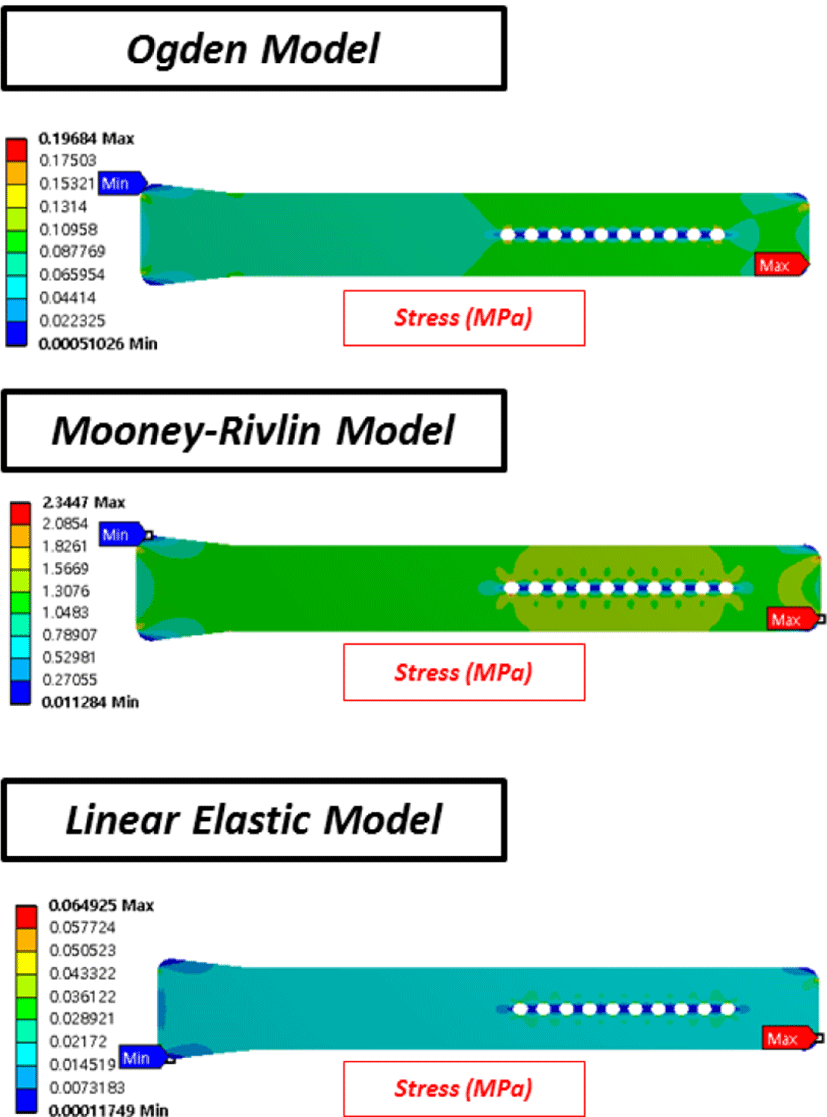
Figure 11에서는 TPE 소재 별 등가응력 값의 변화를 표기하였다. 경도가 낮은 TRIEL 5300NA소재에서의 등가응력 값이 경도가 높은 TRIEL 5550NA 소재에서의 등가응력 값보다 높음을 확인할 수 있다.
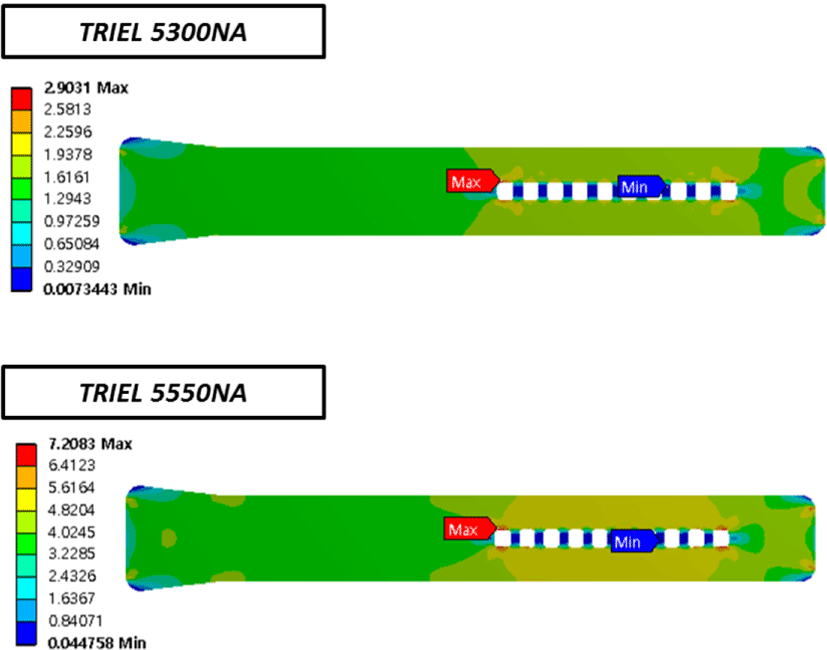
Figure 12에서 변위(Displacement) 변화에 따른 값의 변화를 표기하였다. 실제 변위가 크다는 것(10 mm)은 시편에 가해지는 응력이 더 크다는 것을 의미하는데, 이에 비례하듯 등가응력 값도 유의미한 차이를 보이는 것을 확인할 수 있다.
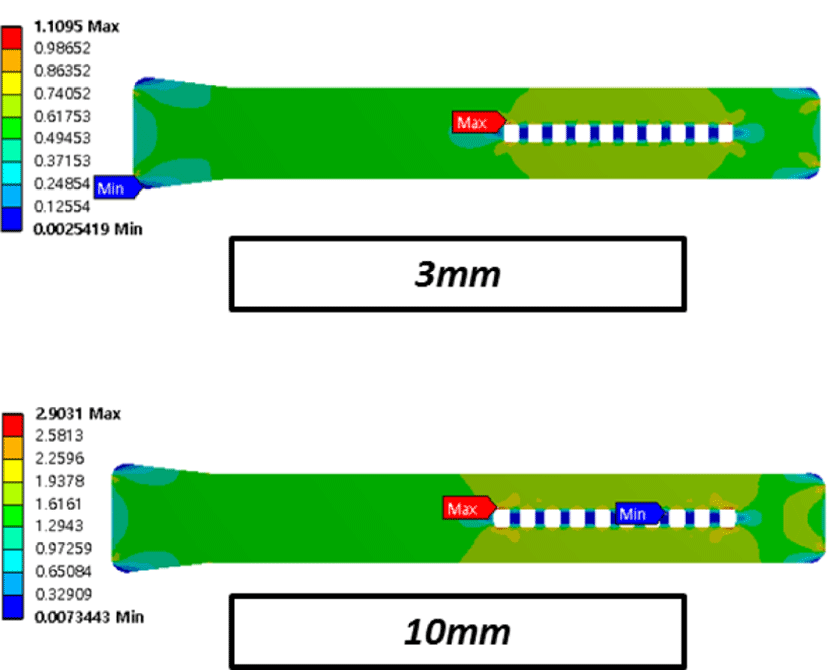
Figure 13에서는 design model 3번의 변형 모델들에 대한 등가응력 값을 표기하였다. 실제 비교 결과는 후술하겠지만, design model 3번에서의 변형 및 stress 변화가 다른 design model 대비하여 큰 것을 확인할 수 있었는데, 이를 개선하고자 추가적인 해석을 진행 하여 결과를 확인해 보았다. 해석 결과 등가응력 값의 변화가 크지 않았으며, 해석 상 최대 변형이 발생하는 위치의 변화가 생겨 실제 양각 및 음각을 적용하였을 때의 취약 부위를 확인 할 수 있다.
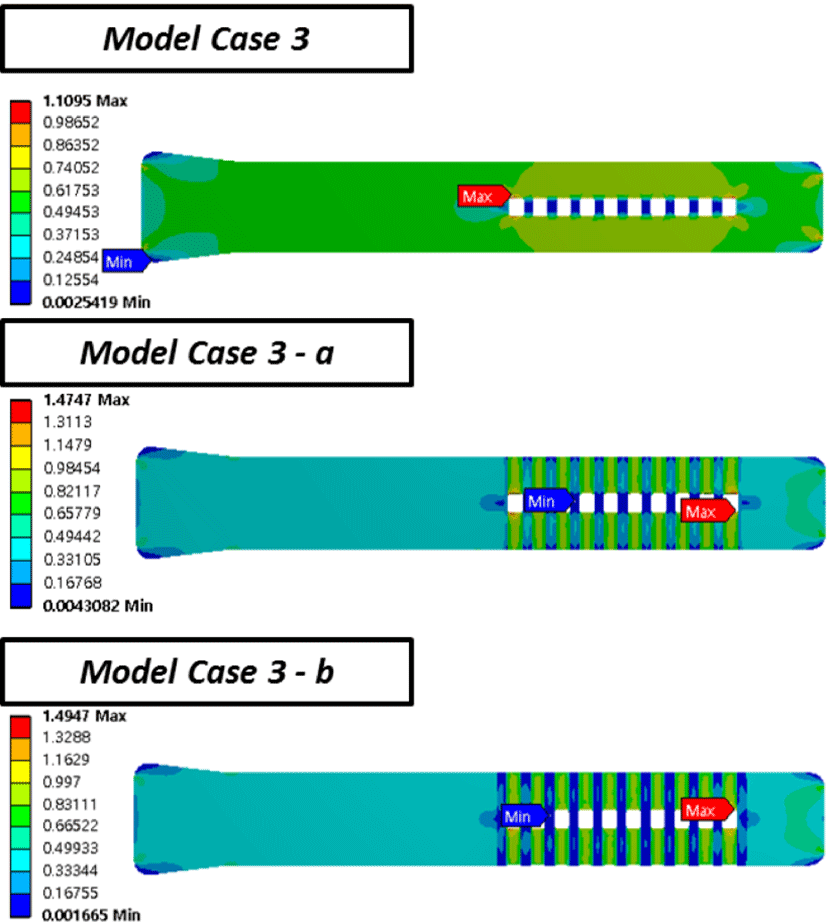
Figure 14에서 각 디자인 모델 별 등가응력 변화를 결과로 정리하였다. 각 소재에 따른 등가응력 차이는 디자인 모델에 따라 차이가 없었으나, material model에 따른 차이는 매우 큰 것을 확인하였다. 실제 제품에 가해지는 압력 대비 Ogden model이나 선형 탄성 모델은 값의 편차가 나타나지 않았으며, 이는 material model의 정합도가 떨어지는 것으로 이해할 수 있다. 이는 앞에서 볼 수 있듯이 실제 인장-변형 데이터의 curve fitting 상에서 차이를 보이는 것과 연결해 생각 해 볼 수 있다. Mooney-Rivlin model의 등가응력 값은 TPE 경도에 따라, 또는 변위 변화에 따라 일정 값으로 변화하는 것을 알 수 있는데, 수치가 큰 것을 고려하더라도 해석 데이터의 정합도가 높음을 확인할 수 있다.
마찬가지로 Figure 15에서는 TRIEL grade에 따른 각 모델의 등가응력 변화 정도를 표기하였다. Material model을 서로 비교한 결과 앞서 서술한 대로 Ogden model이나 선형 모델의 경우 값의 편차가 나타나지 않았으며 이는 마찬가지로 정합도의 차이로 이야기 할 수 있다.
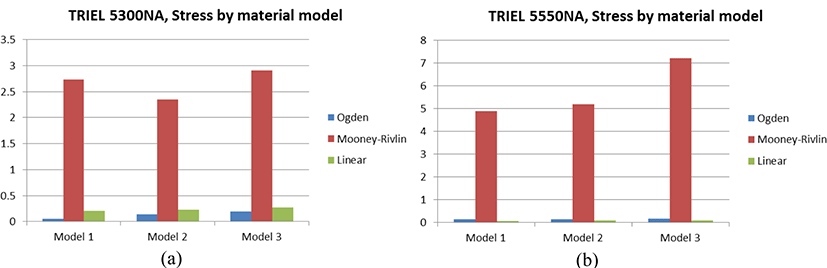
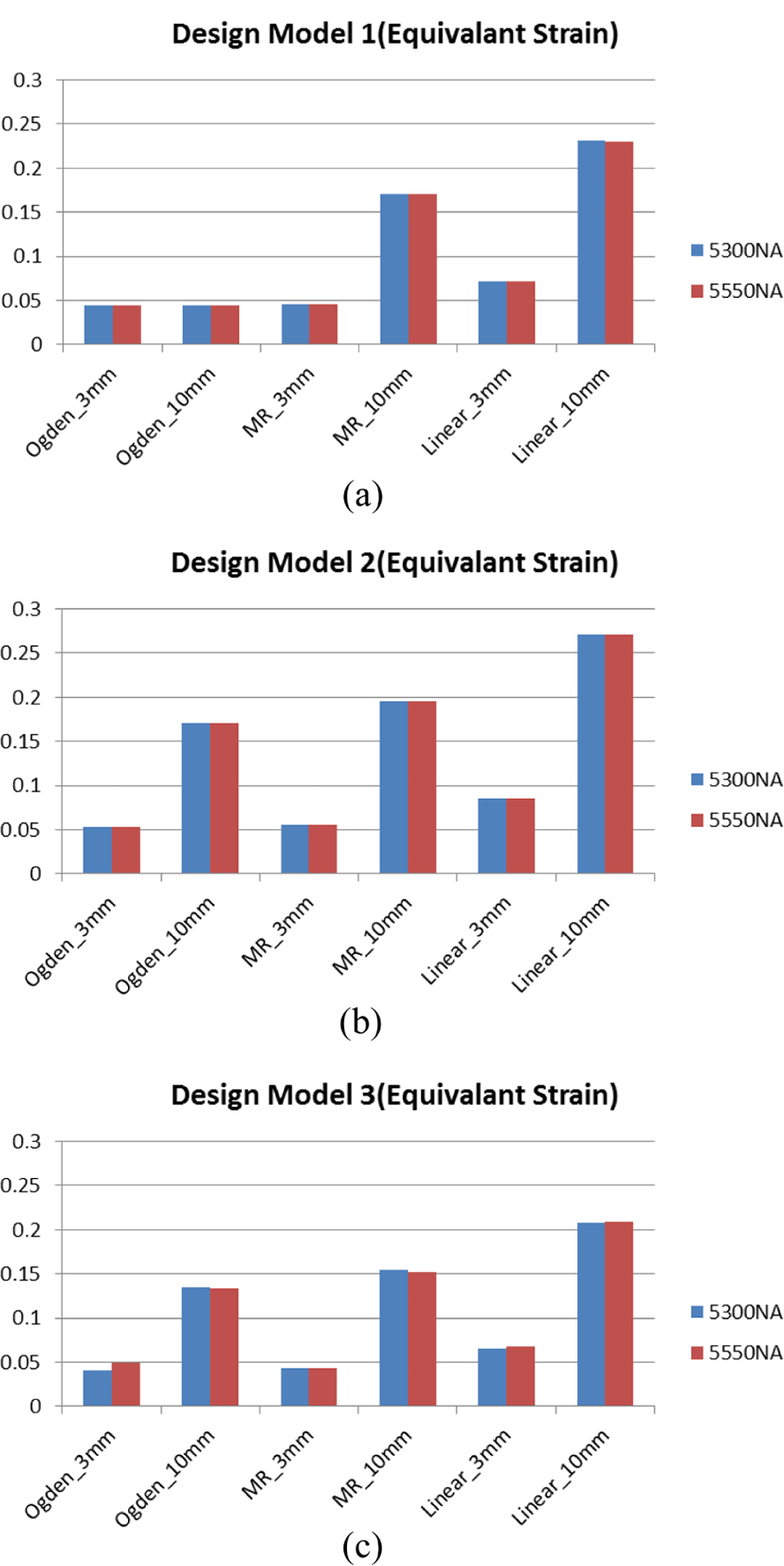
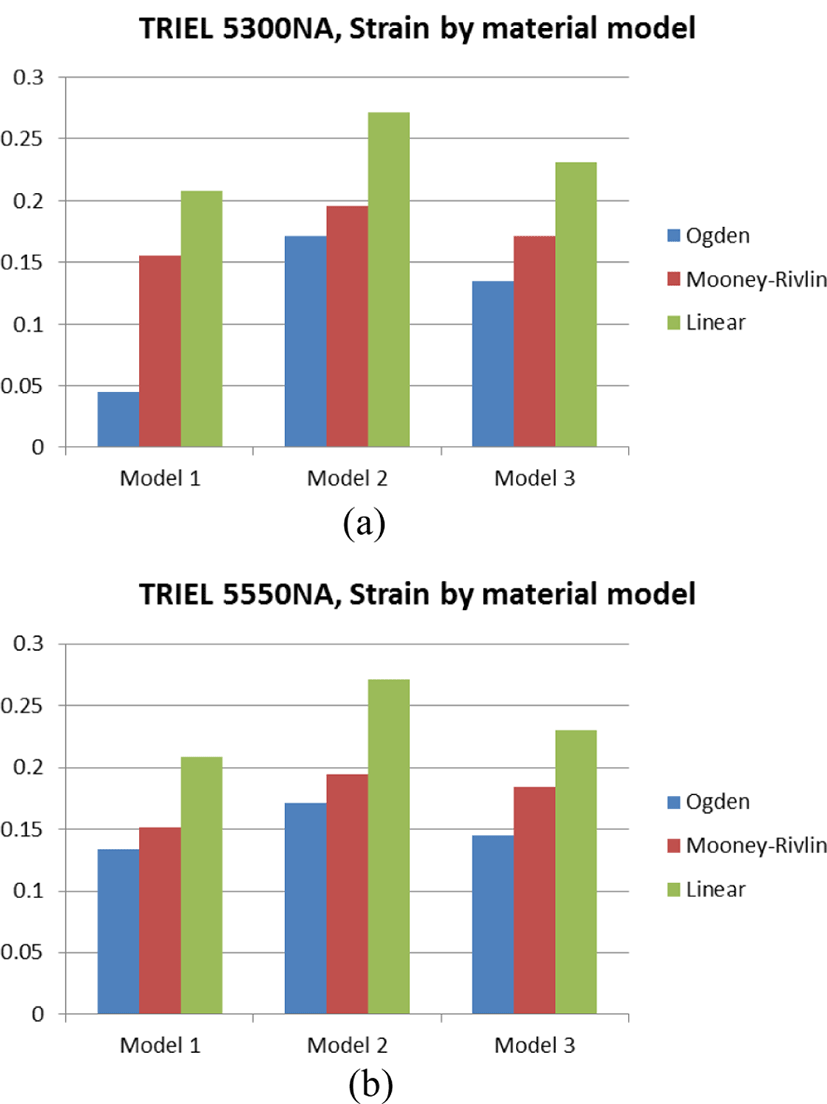
Figure 16과 17에서는 등가변형율(equivalent strain)의 변화 정도를 마찬가지로 정리하였으며, 이는 등가응력과는 조금 별개로 변위에 따라 변화하는 것을 확인할 수 있다. 초탄성 모델 대비 선형 탄성 모델의 변형 값이 더 큰 이유는 선형 모델의 경우 인장-변형의 값은 비례관계이며, 이는 응력이 커질수록 변형도 비례적으로 커지기 때문임을 확인할 수 있다.
마지막으로 Figure 18에서는 design model 3번의 변형 모델에 대한 등가응력 값의 변화 정도를 마찬가지로 정리하였다.
Material 모델에 따른 해석 결과, 우리사 소재를 사용하는 제품에서는 Mooney-Rivlin model의 경우 가장 해석에 적합하다고 할 수 있다. 다른 모델의 경우 데이터의 차이가 발생하는 이유는 실제 인장-변형 곡선의 데이터와의 커브 피팅에서 차이가 있거나, 단순 선형 탄성 해석 방정식을 이용하였기 때문으로 보여진다.
디자인 별 모델에 따르면, 구멍이 아무것도 없는 밴드의 경우에는 이상 변형이 발생할 수 있는 여지가 적기 때문에, 양 끝 단에서 가장 높은 힘을 받는 것을 확인할 수 있으며, 실제 이상 변형이 발생할 수 있는 구멍을 지닌 모델 2, 3번에서는 구멍 주변에서의 등가응력 값이 가장 높게 나오는 것을 확인 할 수 있었다. 이는 구멍이 있는 구조에 따라 디자인 적 약점이 발생 할 수 있다는 것을 의미하며, 이를 해결하기 위해 내부 디자인 변경을 진행해야 할 것으로 보인다.
원형 구멍 모델 대비 사각형 구멍 모델의 응력이 큰 것을 확인 할 수 있었는데, 이는 사각형 구멍의 구조상 직선적인 변위에 좀 더 취약함으로 이해할 수 있으며, 이를 해결하기 위해 양각/음각의 구조적 특이점을 주었지만 이로 인해 응력의 감소가 이루어지지는 않음을 확인하였다.
Conclusions
본 연구에서는 웨어러블 디바이스를 위한 손목밴드의 디자인 및 재료모델에 따른 컴퓨터 해석을 수행하였다.
밴드의 디자인은 홀의 형상에 변화를 주었고, 소재는 TPE로 초탄성 재료모델과 선형 탄성모델을 사용하였다.
디자인에 따라 변화하는 등가 응력 분포를 보면, 일반적으로 예상하는 바와 같이 내부에 구멍(hole)이 없는 디자인의 경우 응력이 고른 분포를 보이는 것을 확일 할 수 있으며, 내부에 구멍이 존재하는 디자인에서는 구멍의 모양에 따라 응력 분포가 변화하는 것을 확인하였다. 실제 구멍의 위치가 동일한 상황에서 원형 구멍의 경우가 사각 구멍의 경우보다 낮은 등가응력 값을 보이는 것을 확인하였으며, 이는 사각형 모양의 구멍이 원형 구멍에 비해 안정성이 떨어진다고 볼 수 있다.
재료 모델에 따른 응력 분포를 보면, Ogden모델과 선형 탄성 모델에서는 응력의 값이 예상 값 보다 현저하게 낮은 것을 확인하였다. 이는 재료 해석 모델이 실제 인장-변형 곡선과의 정합도가 낮기 때문으로 해석된다. Mooney-Rivlin 모델의 경우 변위에 따른, 재료 소재에 따른 응력 분포 변화가 명확하였으며, 이는 실제 인장-변형 곡선과 해석 모델과의 정확도가 높기 때문으로 보이며, 삼양사 소재의 경우에 적합하다고 이야기 할 수 있다.