Introduction
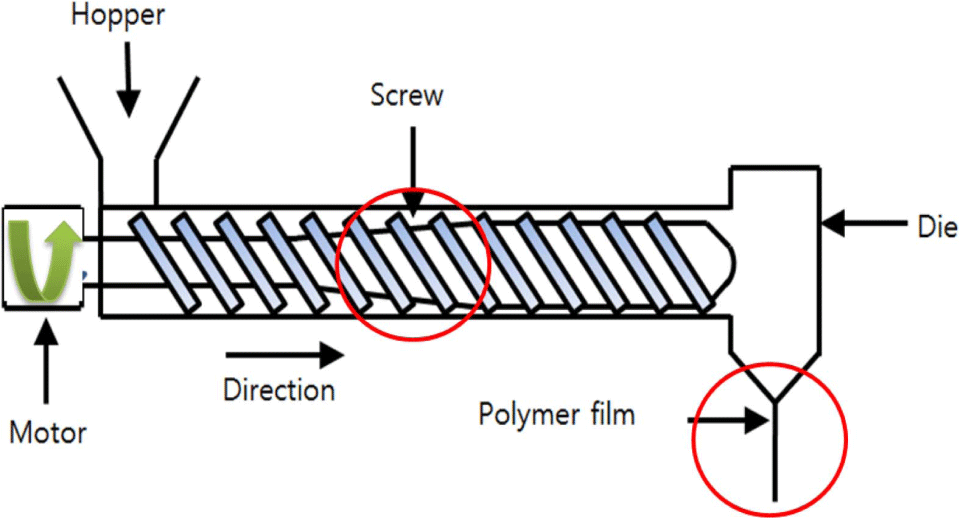
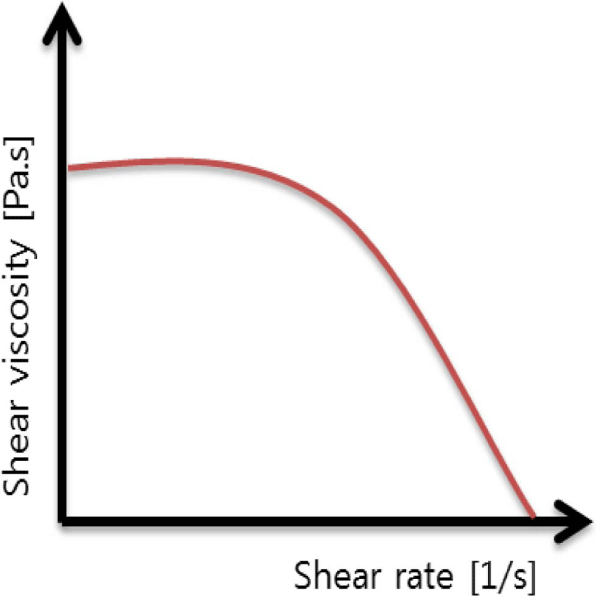
압출 공정은 Figure 1과 같이 호퍼(Hopper)에 고분자 재료를 투입하여 스크류 회전과 압력의 차이를 통해 다이에서 일정한 단면을 가진 연속적인 제품을 생산하는 공정으로, 고분자 재료의 유변학적 특성인 전단 농화(Shear thinning) 현상을 이용하여 필름이나 시트 등으로 생산한다. 전단 농화 현상은 Figure 2과 같이 점도가 일정한 뉴턴 유체와 달리 전단변형률속도가 커지면서 점도가 낮아지는 현상을 말한다. 스크류의 회전에 의해서 고분자 재료의 전단변형률속도가 증가하게 된다. 전단변형률속도가 증가함에 따라 호퍼에 투입될 때 딱딱했던 재료가 점도가 낮아지면서 끈적한 액체에 가깝게 변하게 된다. 이런 현상을 통해 고분자 재료를 원하는 제품의 형상으로 가공이 가능하게 된다.
압출공정에서 가장 중요한 것은 생산성과 제품의 균일성이다. 제품의 생산성은 재료의 유변학적 특성과 공정 조건, 스크류와 다이 형상과 밀접한 관계를 가지고 있다. 제품의 균일성은 압출물의 두께가 일정하게 유지하는 것을 의미하는데 이것은 다이 출구에서의 속도 분포의 균일성과 밀접한 관련이 있다. 압출 공정에서 생산성과 균일성을 동시에 만족시키기 위해서 생산성을 결정짓는 스크류 특성, 다이 특성에 대한 연구와 제품의 균일성을 좌우하는 다이 최적화 연구가 많이 진행되고 있다. 기존의 연구들은 수치해석을 통해 스크류와 다이를 분리하여 각각의 특성에 대한 연구가 많이 진행되어 왔다.1-7 다이 최적 설계에 대해 유한요법으로 해석한 논문도 다이 부분을 최적 설계하였다.8 실제 압출 공정과 동일한 조건인 스크류와 다이를 동시에 해석하는 수치해석 연구는 미미하다. 스크류와 다이를 분리한 연구가 많이 진행되는 이유는 컴퓨터 발전하기 전 과거에는 전체를 3차원적으로 동시에 해석하는 것이 어려웠기 때문이다.
본 논문에서는 스크류와 다이를 동시에 해석을 진행하여 다이 출구의 속도 분포가 일정한 다이 형상 최적화를 진행하였다. 다이 형상 최적화 진행을 위해서 Ansys DesignXplorer 프로그램을 사용하였다.
Die Shape Optimization
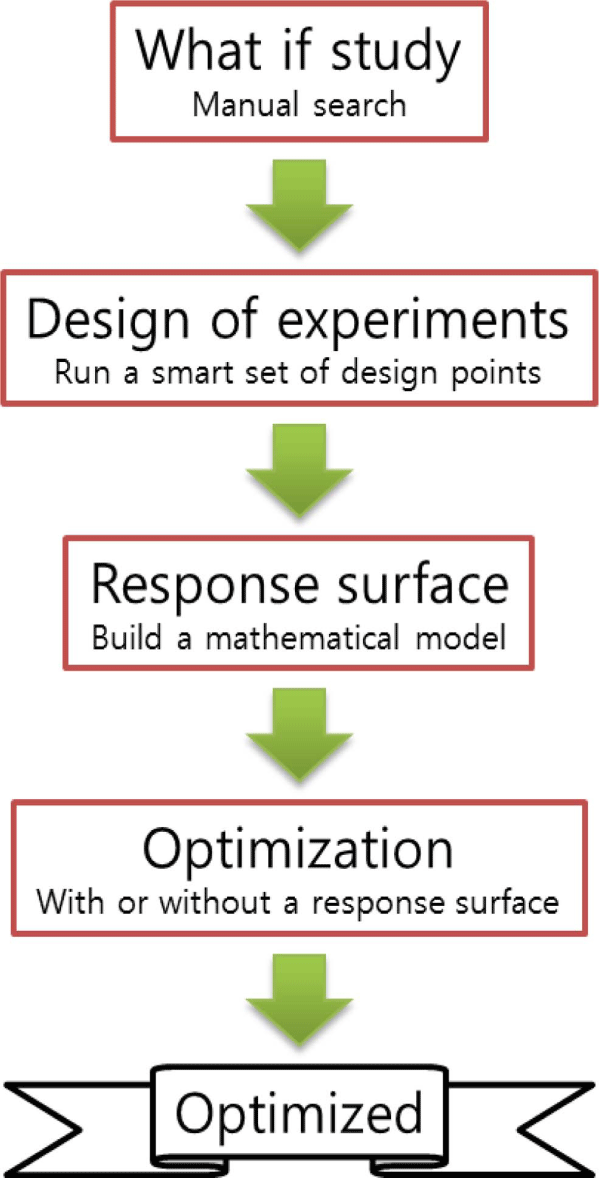
일반적으로 다이 출구의 속도가 균일하지 못하면 압출물이 균일하지 못해 불량품이 생산되며 다이 내부에 허용 압력에 비해 큰 압력이 다이에 작용을 하게 되면 다이가 파괴 될 수 있다. 이러한 문제점들은 보통 압출기의 무리한 운전 또는 다이 형상으로 인해 문제가 발생한다. 다이의 출구 속도의 균일성과 내부 압력을 만족시키는 다이를 만들기 위해서는 다이 형상의 최적화가 필요하다. 여러 공정 조건과 제약 조건을 만족시키기 위해 최적화는 프로그램을 사용하게 된다. 최적화에 사용된 프로그램 중 Ansys DesignXplorer를 일반적으로 사용한다. 최적화 프로그램은 Figure 3과 같은 순서로 진행한다.
실험 설계(Design of experiments)는 응답 표면(Response surface)을 계산하기 위한 대표적인 데이터 집합을 모으는 역할을 한다. 여기서 데이터 집합을 디자인 포인트라고 하는데 이것은 자동적으로 계산한다. 다음 과정인 응답 표면은 실험 설계의 계산된 디자인 포인트 수에 따라서 정확도가 크게 달라진다.
응답 표면은 대리 모델(Surrogate model) 또는 근사 모델(Approximation model)이라고 한다. 응답 표면은 출력 매개 변수(Output parameter)와 입력 매개 변수(Input parameter)의 관점에서 설명하는 다른 특성 함수이다. 응답 표면은 실험 설계에서 여러 값들을 분석하여 출력 매개 변수의 근사 값을 제공하게 된다. 응답 표면의 결과 값으로는 응답 포인트(Response points), 최소-최대 검색(Min-max search), 응답 차트(Response chart) 등이 있다.
응답 포인트의 결과 값은 응답 표면에서 예측한 근사 결과 값을 나타낸다. 테이블에 입력 값을 입력하거나 변경하게 되면 즉시 출력 값에서 결과를 알 수 있다. 최소-최대 검색은 입력 값의 변화에 따른 출력 값의 최소 값과 최대 값을 나타낸다. 응답 차트에서는 입력 값에 대한 출력 값의 변화를 응답 차트(Resonse chart), 지역 민감도(Local sensitivity)와 지역 민감도 곡선(Local sensitivity curves), 거미 차트(Spider chart) 등으로 나타낸다. 지역 민감도는 막대 차트로 나타내며 막대 차트의 각각의 값은 다음과 같이 계산하게 된다.
응답 차트는 입력 값과 출력 값을 2D, 3D 그래프로 나타낸다. 2D 그래프는 입력 값(x축) 변화에 따른 출력 값(y축) 변화를 나타낸다. 3D 그래프는 2개의 입력 값(x축, y축)에 대한 출력 값(z축)의 변화를 나타낸다. 지역 민감도 곡선은 다른 모든 입력 값을 고정하고 한 개의 입력 값의 변화에 따른 출력 값의 감도를 나타낸다. 여기서 x축은 변경되는 입력 값이고 y축은 감도이다. 거미 차트는 입력 값의 변화에 따른 모든 출력 값을 시각적으로 낸다.
마지막 단계인 최적화(Optimization)은 응답 표면 최적화와 달리 출력 값에 대한 근사 값을 나타내는 것이 아니라 실제 계산 결과를 출력 값으로 나타내는 것이다. 최적화의 방법은 선별(Screening),9 다목적 유전 알고리즘(Multi-Objective genetic algorithm),10 이차 라그랑지안 비선형 프로그램(Non-linear programming by quadratic lagrangian)11 등이 있다. 여러 최적화 방법 중 가장 기본적으로 선별 방법을 사용한다. 선별 방법은 응답 곡선에서 계산한 근사 값들을 목표, 가중치 및 제약 조건을 기준으로 원하는 값을 선별하게 된다. 원하는 목표, 가중치 및 제약 조건을 설정하게 된다.
최종적으로 모든 제약 조건을 만족하는 입력 값과 출력 값이 표에 나타나게 되는데 여기서 제약 조건에 가장 적합한 값들은 별표로 나타낸다. 제약 조건을 만족한 값들 역시 근사 값이기 때문에 최적 조건에 가장 부합하는 값을 선택하여 검증 해석을 실시한다. 검증 해석 후 근사 값과 근접하게 되면 최적화는 완료된다.12
Analysis Conditions
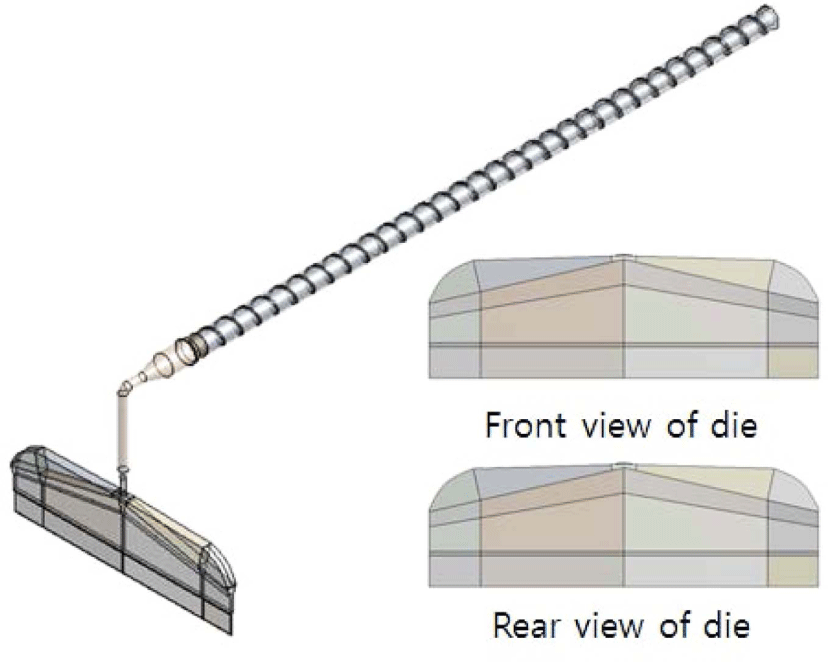
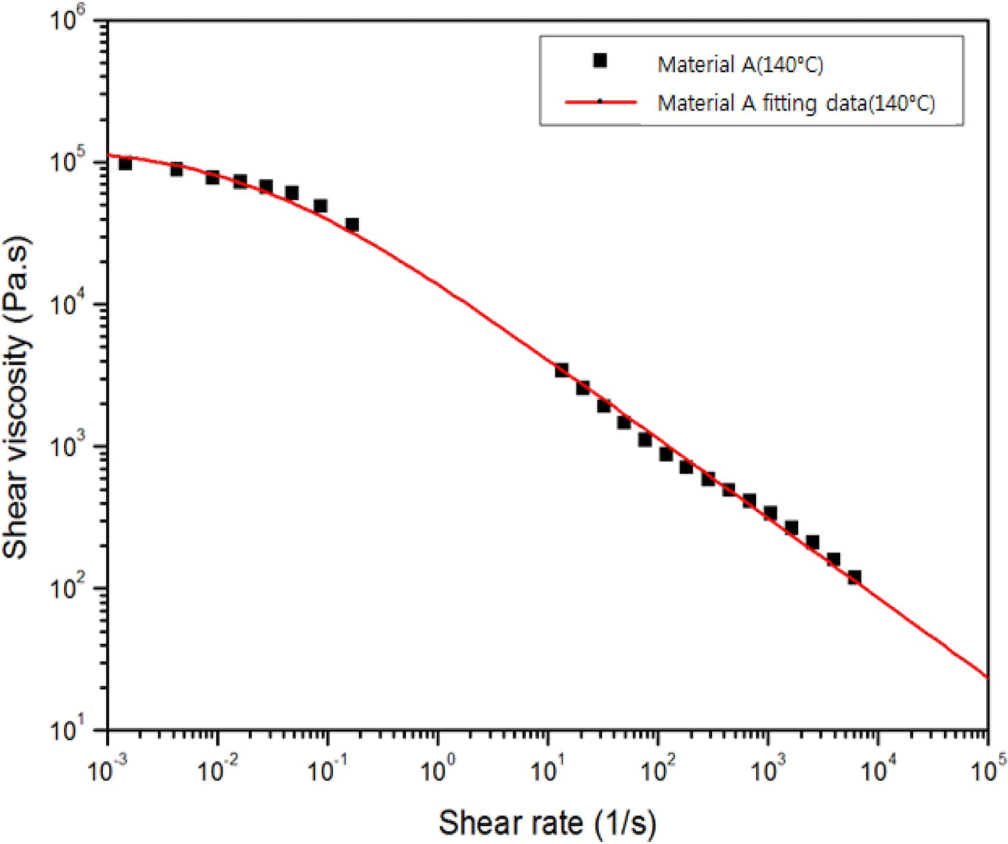
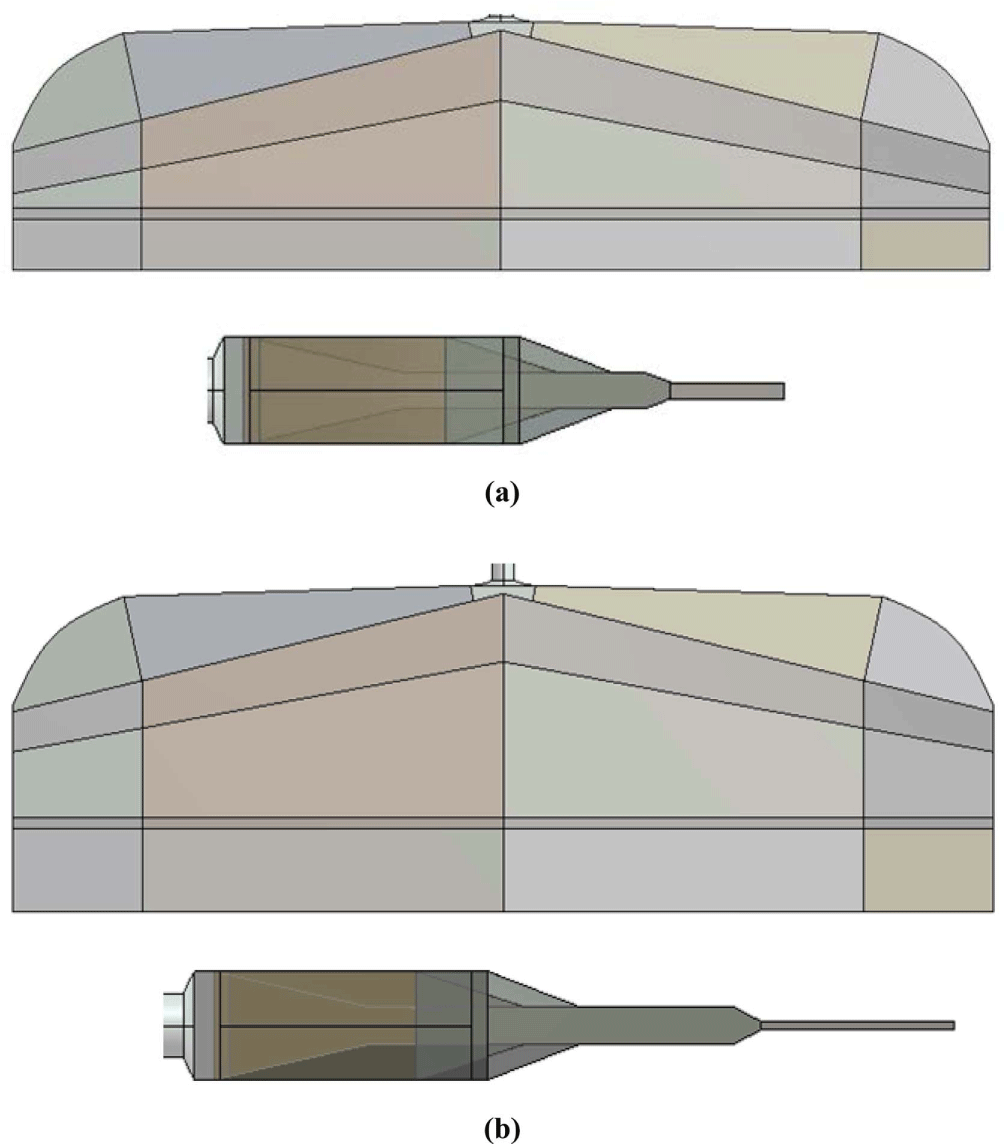
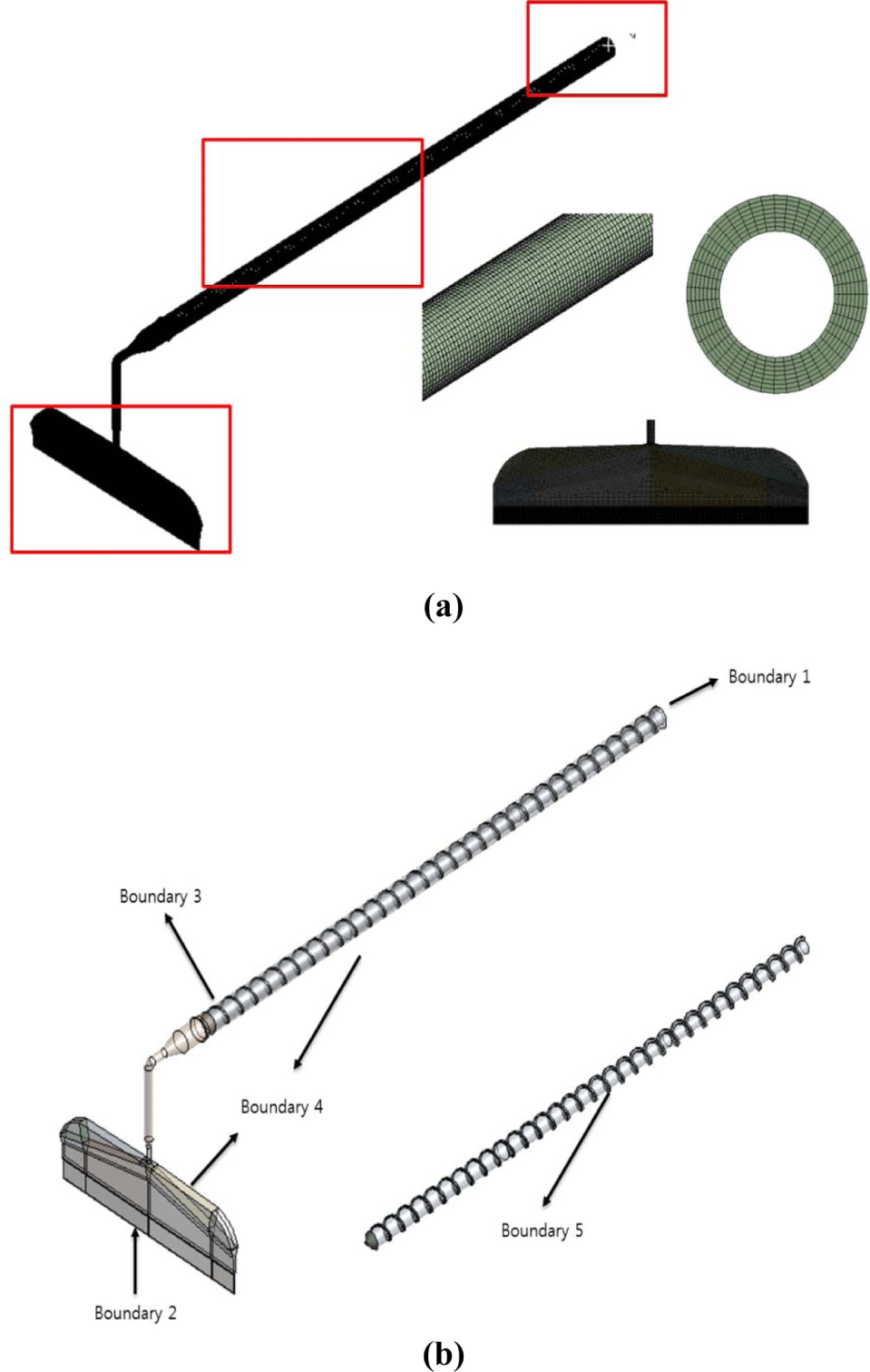
다이 형상 최적화 해석에는 Figure 4와 같이 스크류, 다이 모두 포함하는 압출기 형상에서 다이는 평판 다이로 선택하여 최적화에 사용하였다. 평판 다이는 James Allen의 연구에 사용된 다이이며 앞면과 뒷면이 대칭이다.8 James Allen의 연구에 사용된 평판 다이는 본 연구에 사용된 압출기의 크기와 차이가 크기 때문에 압출기와 크기를 비슷하게 하기 위해 60%로 축소하였다. Figure 5(a)는 스크류와 다이 형상의 격자 형상을 나타낸다. 형상의 격자는 스크류 특성, 다이 특성 해석과 동일하게 격자를 만들었다. Figure 5(b)와 Table 1은 다이 최적화 해석의 경계 조건을 나타낸다. 경계 조건은 압출기 해석과 동일한 경계 조건을 사용하였다. 스크류의 회전 속도는 40 rpm로 설정하였다. 해석에 사용된 물성은 Figure 6과 Table 2과 같이 Cross model에 피팅한 값이며 이 물성과 동일한 물성을 사용하였다.
| Material a (isothermal) | |
|---|---|
| Parameters | Value |
| η0 = Zero –shear rate viscosity | 133307[Pa.s] |
| λ = Natural time | 46.6409[s] |
| n = Cross model index | 0.563047[-] |
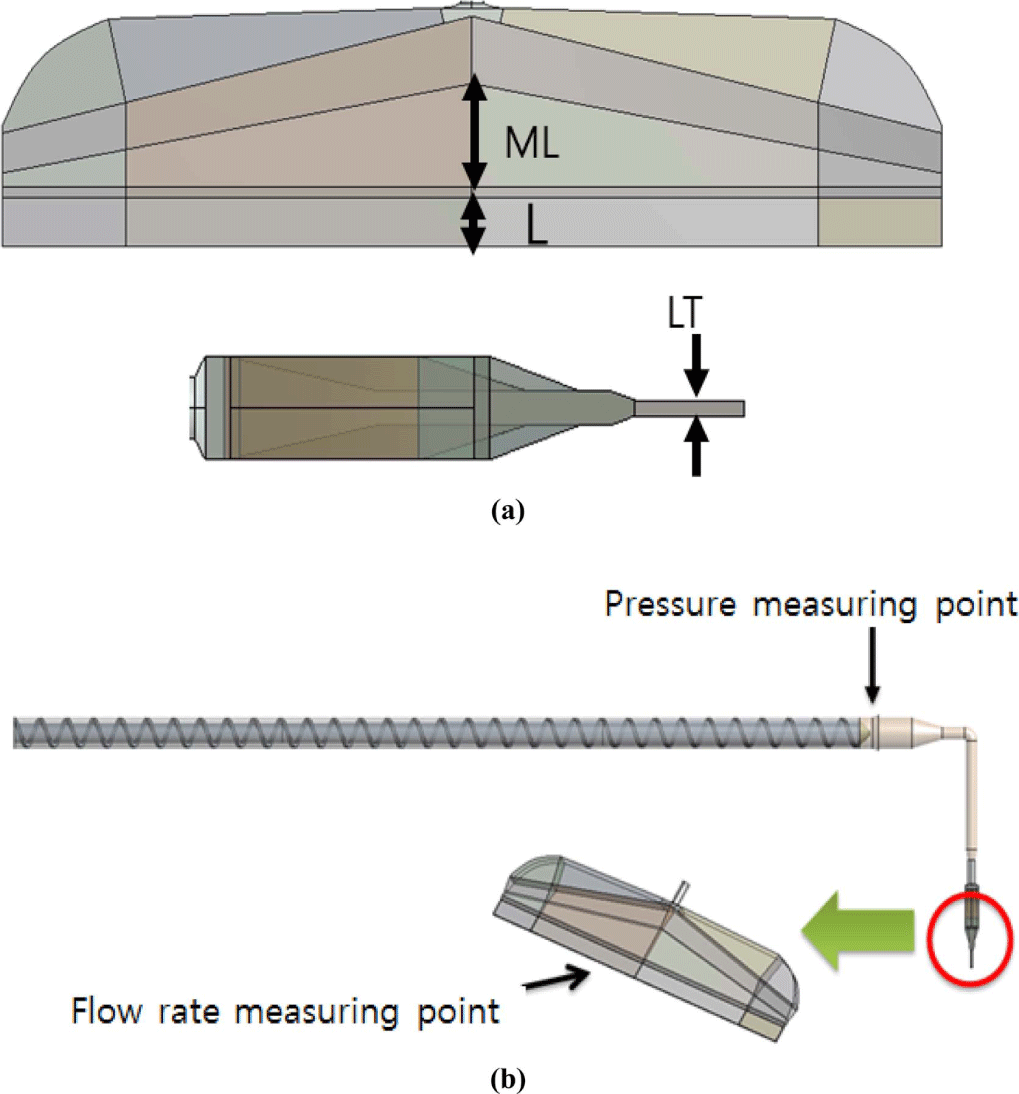
다이 형상 최적화에 사용된 평판 다이는 James Allen의 연구에서 해석 결과 출구 속도 분포가 균일하지 않아 In-Equality penalty 알고리즘과 Equality penalty 알고리즘을 이용하여 최적화하였다.9 본 논문은 James Allen의 논문과 동일한 알고리즘을 사용하지 않고 최적화 프로그램 중 상용 소프트웨어인 Ansys DesignXplorer를 사용하였다. 실험 설계에 기본적인 중앙 복합 디자인(Central composite design) 모델을 사용하였다. 응답 표면에서는 Kriging 모델 사용하였고 최적화에는 응답 표면 최적화(Response surface optimization)을 선택하였다. 실험 설계에서는 다이의 형상 변경 부분을 설정하고 최대 값과 최소 값을 선택하여야 한다. Figure 7(a)는 평판 다이의 최적화 시 변경 할 부분을 나타내며 Table 3(a)는 기본 형태의 치수를 나타낸다. Table 3(b)는 형상 변경의 최대 값과 최소 값을 나타낸다. 해석 결과에서는 매니폴드의 길이(Manifold length)의 변경 값을 길어진 치수로 나타냈으며 기본 길이를 1[mm]로 나타냈다. 최소 값은 -5[mm], 최대 값은 31[mm]로 환산이 된다.
| (a) | |
|---|---|
| Name | Length(mm) |
| ML(Manifold length) | 60 |
| L(Land length) | 28 |
| LT(Land thickness) | 3.6 |
| (b) | ||
|---|---|---|
| Name | Min(mm) | Max(mm) |
| ML(Manifold length) | 54 | 90 |
| L(Land length) | 2 | 7 |
| LT (Land thickness) | 8 | 48 |
Results and Discussion
Figure 7에서 (a)는 최적화 하고자 하는 다이 형상의 중요 변수, 즉 ML, L, LT 등을 가시화 한 것이고, (b)는 다이 형상 최적화에서 다이 출구의 속도 분포와 압력 측정 위치를 나타낸다. 여기서 ML은 매니폴더(Maniford) 길이(ML)를 LT는 랜드 두께(LT), L은 랜드의 길이(L)를 의미하며 다이 출구의 속도 분포는 다이 출구의 두께 방향의 중앙 부분에서 폭 방향으로 선을 생성하여 측정하였다. 압력은 스크류 끝단의 평균 압력을 측정하였다.
Figure 8(a)는 초기 평판 다이의 압출 해석 결과이다. 초기의 평판 다이의 출구 속도 분포는 다이 출구의 중앙 부분의 속도는 가장 빠르고 가장자리의 속도는 가장 느리게 나타났다. 이렇게 중앙 부분과 가장자리의 속도 편차가 크기 때문에 최적화가 필요하다. 다이 형상 최적화를 하기 위해서는 최적화의 목적 함수가 필요하다. 여기서 목적 함수는 다이 출구의 중앙 부분의 속도와 가장자리의 속도 편차와 다이 끝 단의 압력이다. 다이 출구의 속도 편차와 스크류 끝 단의 압력이 가장 작은 것을 만족하는 것이 가장 중요하다. 목적 함수는 Figure 8(b)과 같이 P1과 P2, “Outp” 와 스크류 끝 단의 압력으로 설정하였다. 여기서 P1은 다이 출구의 중앙 부분의 속도이며 P2는 가장자리에서의 속도이다. “Outp”는 다이 출구의 중앙 부분과 가장자리 부분의 속도 편차이다. Table 4(a)은 초기 형상 다이의 목적 함수 값들을 나타낸다.
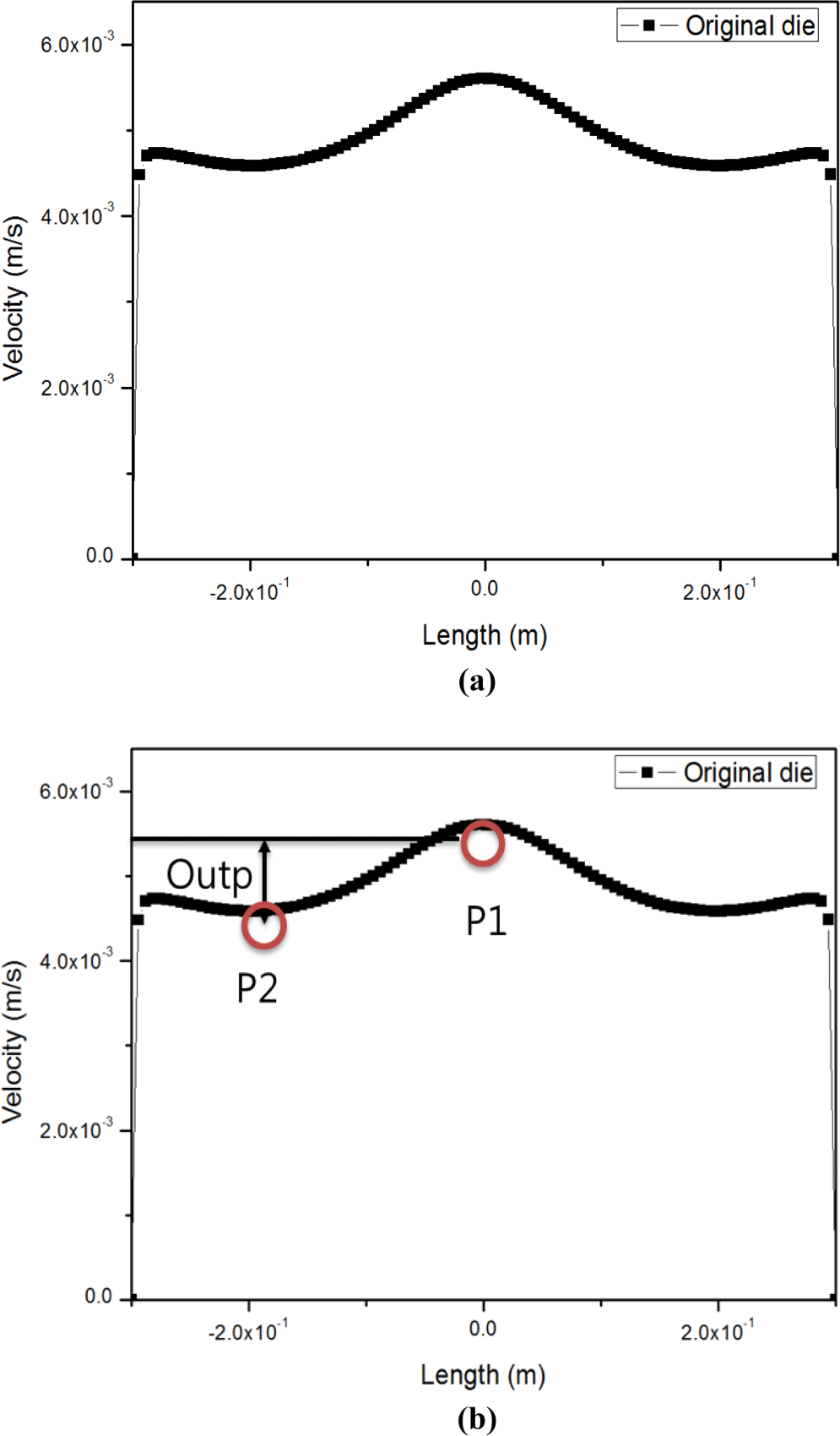
| (a) | |
|---|---|
| Name | Value |
| P1[m/s] | 5.6080×10-3 |
| P2[m/s] | 4.7308×10-3 |
| Outp(P1-P2)[m/s] | 8.7720×10-4 |
| ∆P(Pa) | 4.5941×106 |
최적화의 첫 번째 단계인 실험 설계에서는 Table 4(b)와 같이 다이 변경 부분의 최소 값과 최대 값을 지정하게 되면 다이 변경 치수를 무작위로 설정하여 목적 함수의 값을 계산한다. Figure 9(a), (b)~Figure 13(a), (b)는 최적화의 두 번째 단계인 응답 표면에서 응답 곡선을 나타낸 것이다. 응답 곡선은 실험 설계의 값을 바탕으로 다이 형상 변경에 따른 목적함수의 근사 값들의 데이터를 그래프로 나타낸다.
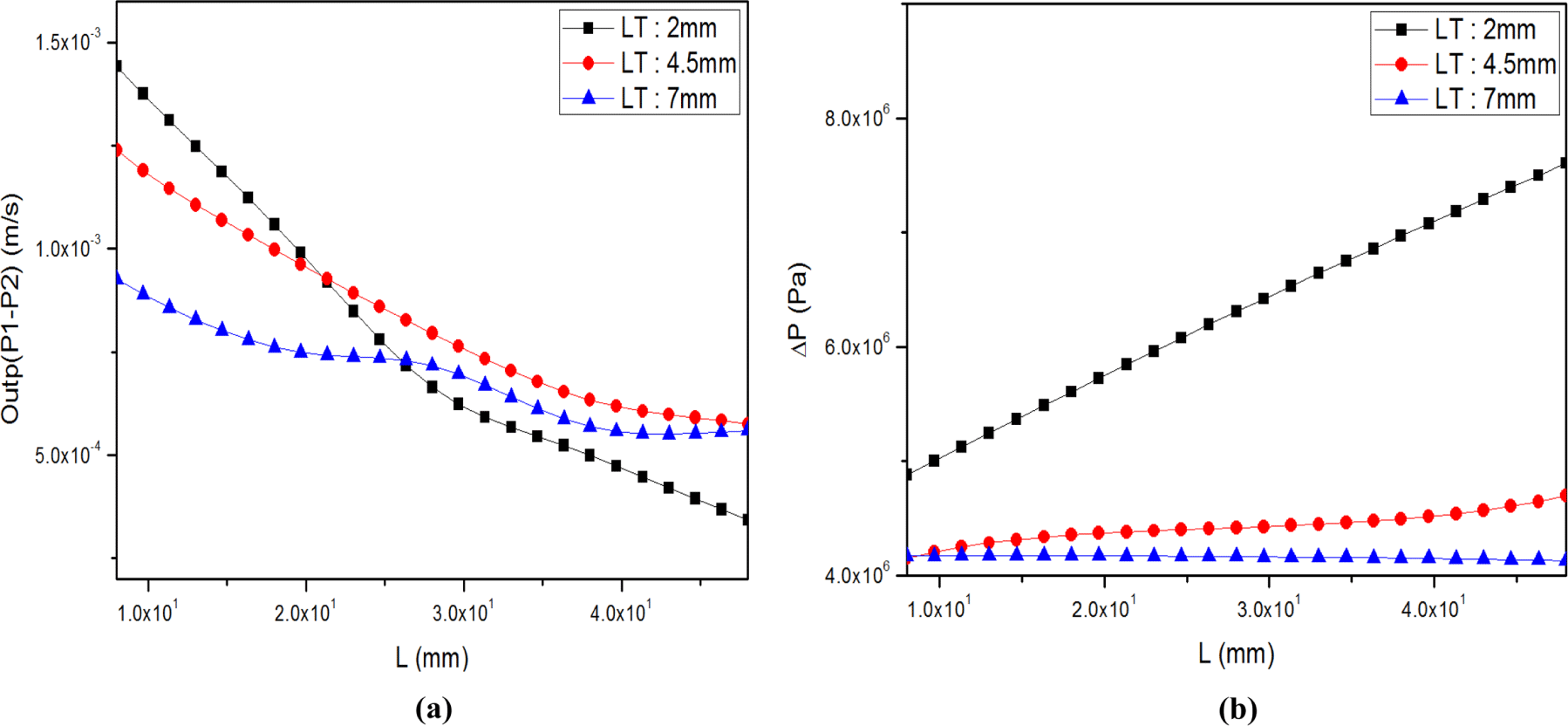
Figure 9(a)는 매니폴더 길이(ML)를 13 mm로 고정하고 랜드 두께(LT)의 최소 값 2 mm, 중간 값 4.5 mm, 최대 값 7 mm로 변경 시 랜드의 길이(L) 변화에 따른 다이 출구 중간의 속도와 가장자리 속도의 편차(“Outp”), Figure 9(b)는 압력 값의 변화를 나타낸 것이다. L이 길어짐에 따라 “Outp”는 증가하고 압력은 감소하는 경향을 보여준다. LT를 최소 값으로 변경할 시 L방향의 길이가 길어질수록 “Outp” 값의 편차 차이가 가장 작아지고 압력의 값이 증가 폭이 크게 나타났다. Figure 10(a)는 LT를 4.5 mm로 고정하고 ML의 최소 값 -5 mm, 중간 값 13 mm, 최대 값 31 mm로 변경 시 랜드의 길이(L) 변화에 따른 다이 출구 중간의 속도와 가장자리 속도의 편차(“Outp”), Figure 10(b)는 압력 값의 변화를 나타낸 것이다. L이 길어짐에 따라 “Outp”는 증가하고 압력은 감소하는 경향을 보여준다. ML 값이 최대값 일 때 “Outp”의 편차 차이가 가장 작고 압력의 증가 폭도 가장 크게 나타났다. 그러나 ML의 변경에 따른 “Outp”편차와 압력의 변화는 미미하였다.
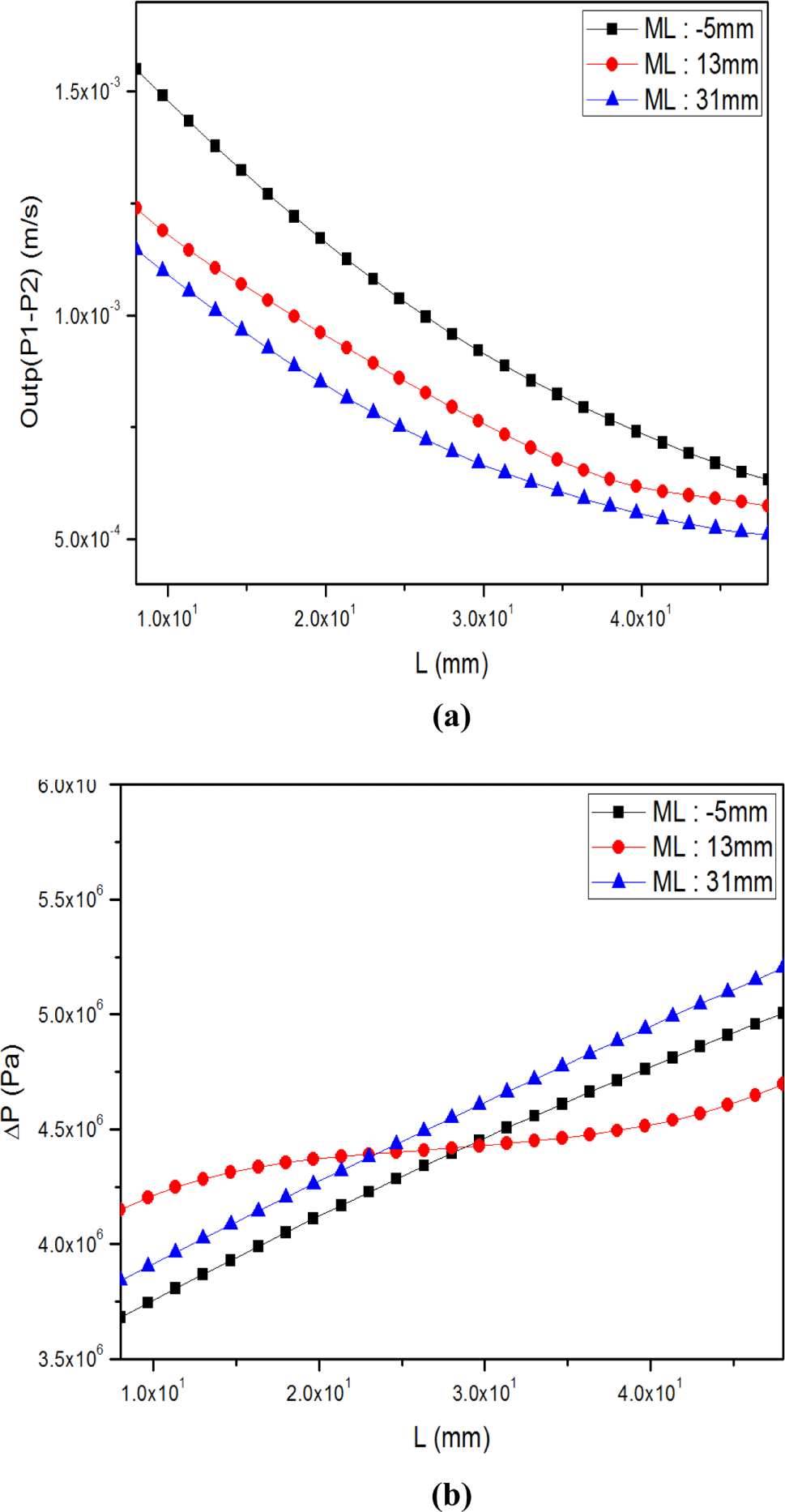
Figure 11(a)은 ML을 13 mm로 고정하고 L의 최소 값 8 mm, 중간 값 28 mm, 최대 값 48 mm로 변경 시 LT변화에 따른 다이 출구 중간의 속도와 가장자리 속도의 편차(“Outp”), Figure 11(b)는 압력 값의 변화를 나타낸 것이다. L의 길이가 중간 값과 최대 값을 가질 때와 최소 값을 가질 때 “Outp”의 편차는 다른 경향을 보여준다. L값이 최소 값일 때 LT이 두꺼워짐에 따라 “Outp”편차가 급격히 감소하는 반면 중간 값과 최대 값은 소폭으로 증가한다. 하지만 LT값이 커질수록 L값의 길이의 변경과 무관하게 “Outp” 편차의 값은 낮게 나타났다. 압력은 L의 값이 최소, 중간, 최대 값 모두 감소하는 경향을 보인다. L값이 최대 값일 때 LT가 두꺼워 질수록 압력 값의 감소 폭은 가장 크게 나타났다.
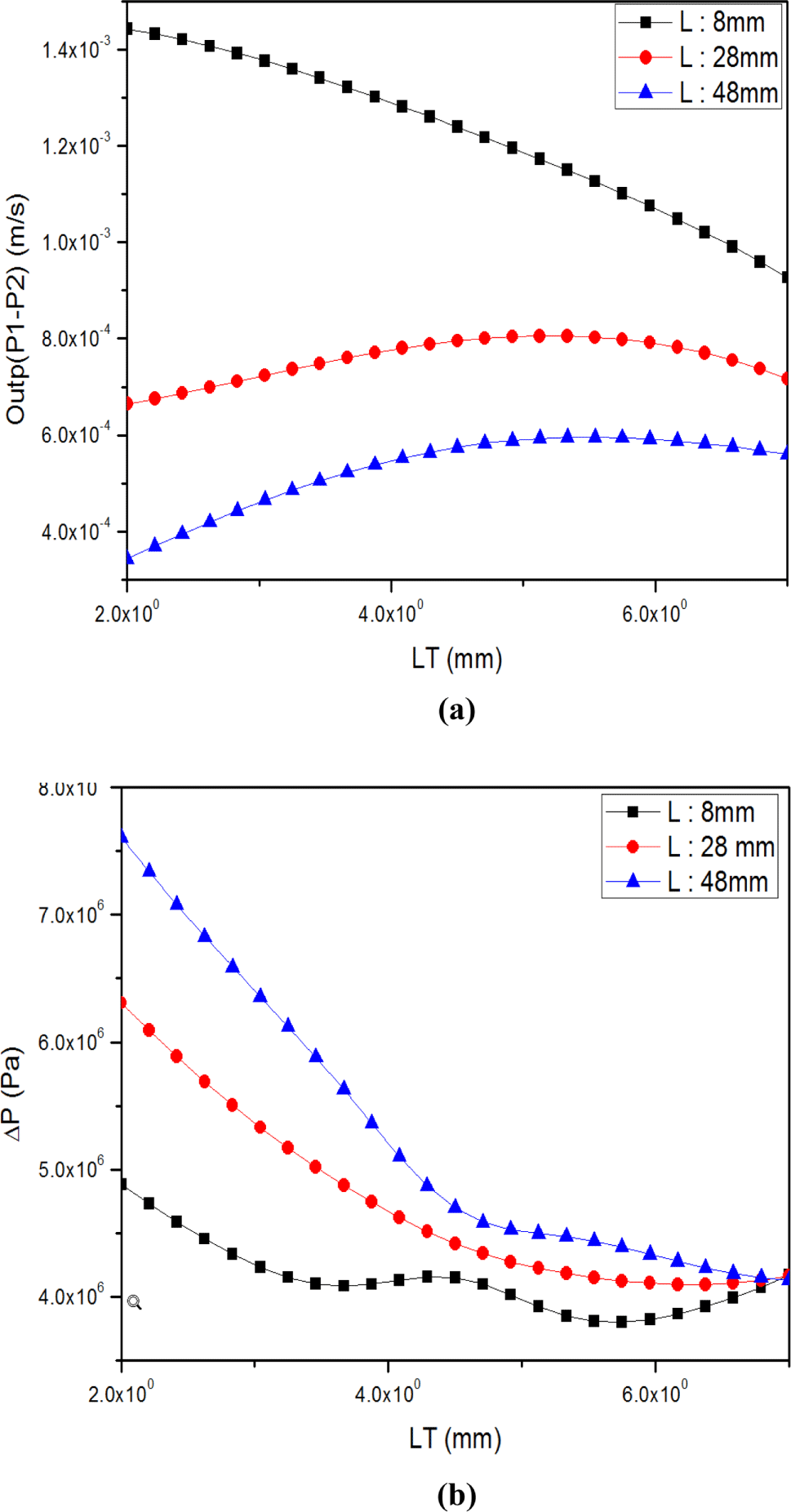
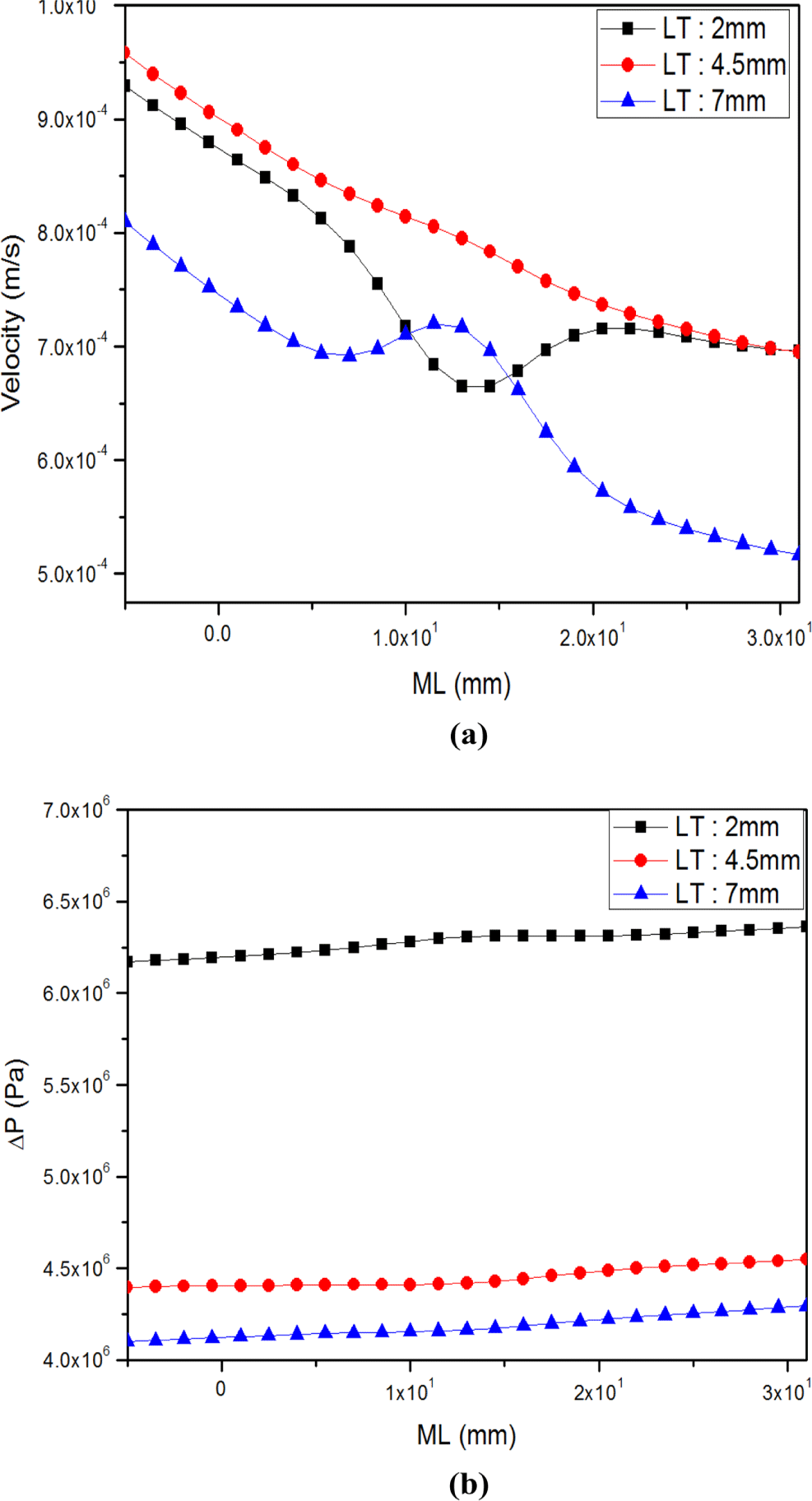
Figure 12(a)는 L을 28 mm로 고정하고 L의 최소 값 -5 mm, 중간 값 13 mm, 최대 값 31 mm로 변경 시 LT변화에 따른 다이 출구 중간의 속도와 가장자리 속도의 편차(“Outp”), Figure 12(b)은 압력 값의 변화를 나타낸 것이다. ML의 값이 최소 값, 중간 값, 최대 값을 가질 때 LT의 변화에 따라 “Outp”의 편차는 크지 않았으나 ML이 중간 값일 때 다른 값과 달리 “Outp”값이 소폭으로 증가하였다. 압력은 ML의 값이 최소 값, 중간 값, 최대 값일 때 모두 LT가 두꺼워짐에 감소하는 경향을 보였으나 ML의 값이 변경되더라도 서로 간의 압력의 감소 정도는 비슷하게 나타났다.
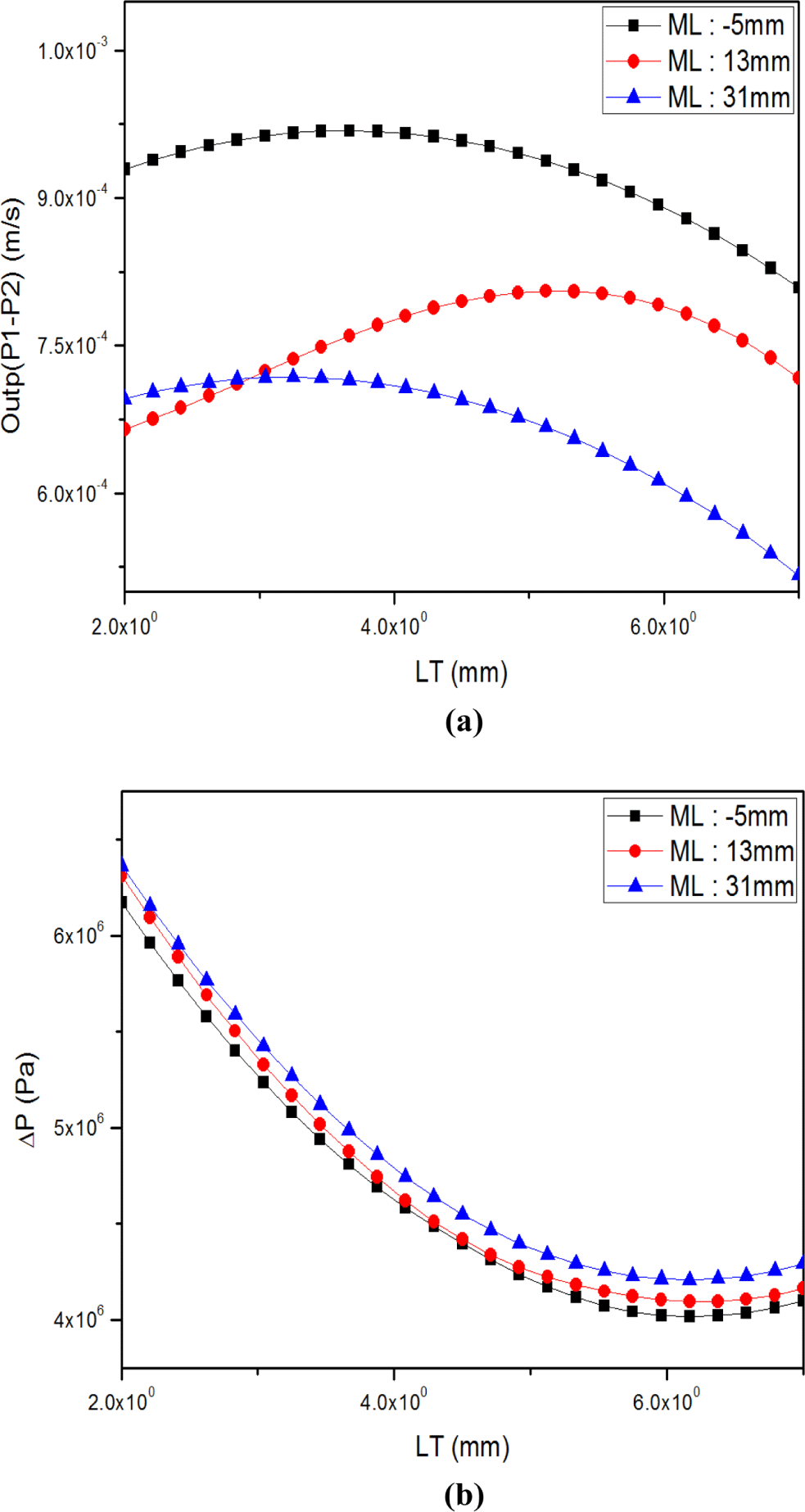
Figure 13(a)은 LT를 4.5 mm로 고정하고 L의 최소 값 8 mm, 중간 값 28 mm, 최대 값 48 mm로 변경 시 ML변화에 따른 다이 출구 중간의 속도와 가장자리 “Outp”, Figure 13(b)은 압력 값의 변화를 나타낸 것이다. ML의 값이 최소 값, 중간 값, 최대 값을 가질 때 “Outp”의 값은 점점 감소하는 경향을 보였으나 감소 폭은 미미하였다. 압력은 L값이 최소 값일 때 ML이 길어짐에 따라 증가 또는 감소하는 것이 아니라 지정한 길이의 중간부분 부에 감소하고 다시 일정하게 유지 되었다. 최대 값 일 때는 ML 최소 값과 반대로 압력이 지정한 길이의 중간 부분에서 증가하였다가 다시 유지되었다.
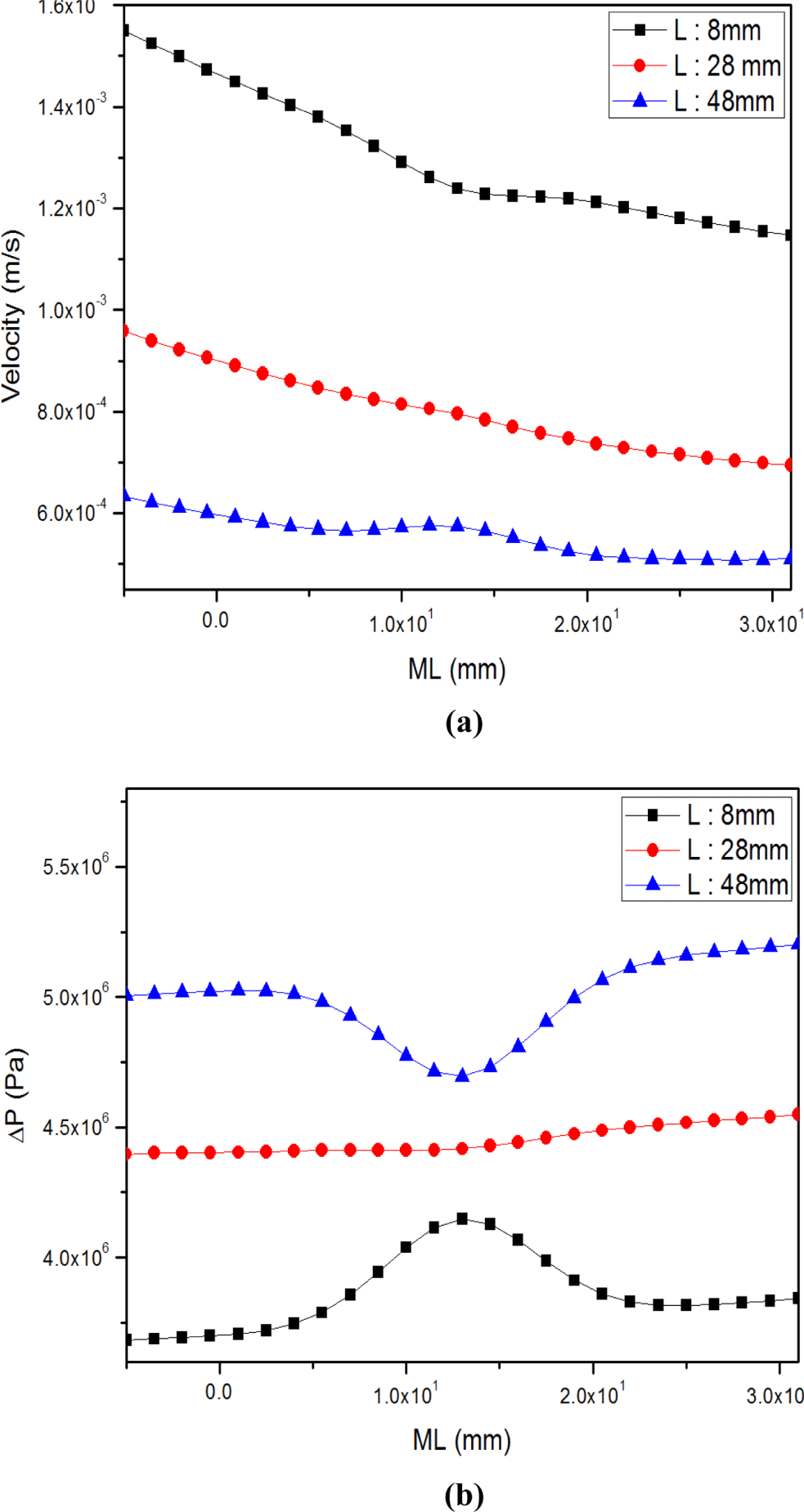
Fgure 14(a)은 L을 28 mm로 고정하고 LT의 최소 값 2 mm, 중간 값 4 mm, 최대 값 7 mm로 변경 시 ML변화에 따른 다이 출구 중간의 속도와 가장자리 “Outp”, Figure 14(b)은 압력 값의 변화를 나타낸 것이다. LT의 값이 최소 값, 중간 값, 최대 값을 가질 때 “Outp”의 값은 점점 감소하는 경향을 보였다. 압력 또한 LT값이 무관하게 일정하게 유지된다.
최적화는 응답 표면의 근사 값을 바탕으로 원하는 최적 설계를 진행하기 위해 제약 조건을 설정하게 된다. 본 논문에서는 “Outp”는 0 m/s에 가까운 값, 압력은 8×106 Pa 보다 낮은 압력을 검색하도록 제약 조건을 설정하였다. Table 5는 설정한 제약 조건을 만족하는 입력 값과 출력 값을 나타낸 것이다. 제시한 값은 근사 값이기 때문에 검증 해석을 실시하여야 한다. 본 논문에서는 “Outp”의 편차가 가장 작고 압력이 7.5×106 Pa 정도인 1번을 선택하여 검증 해석을 실시하였다.
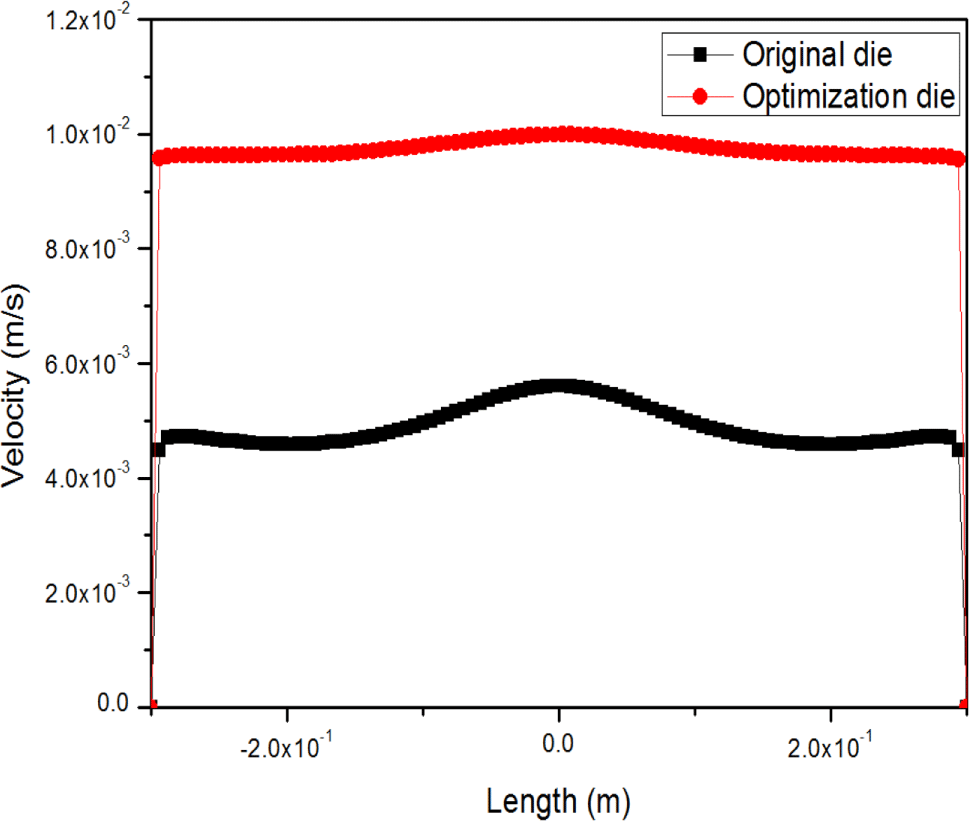
Figure 15(a)은 기존의 평판 다이 형상이고 Figure 15(b)는 검증 해석 후 최적화된 평판 다이 형상이다. Table 6는 기존 다이와 최적화 된 다이의 ML과 L, LT의 치수를 나타낸 값을 나타낸다. 본 논문에서 최적화시 고려하지 못한 것은 압출물의 두께이다. 두께는 압출 공정에서 중요한 부분 중 하나이다. 하지만 압출물의 두께는 압출 공정 이후 필름 캐스팅(Casting) 공정에서 제어가 가능하기 때문에 압출물의 두께 보다 출구 속도의 균일성에 중점을 두고 최적화를 진행하였다. Figure 16은 기존 다이와 최적화된 다이의 다이 출구의 속도 분포를 측정한 것이다. Table 7은 기존 형상과 최적화 형상의 목적 함수 값을 나타낸다. 최종적으로 다이 출구의 속도가 증가하여 압출물의 토출량이 증가하였으며 “Outp”의 값은 현저히 줄어들었다. 압력 구배 또한 실제 공정 조건과 비슷하기 때문에 압출물의 균일성 부분에서는 최적화가 완료되었다.
| Name | Original die | Optimization die |
|---|---|---|
| ML(Manifold length) | 60 | 82.56 |
| L(Land length) | 28 | 48 |
| LT(Land thickness) | 3.6 | 2 |
| Name | Orignal die | Optimization die |
|---|---|---|
| P1[m/s] | 5.608×10-3 | 9.990×10-3 |
| P2[m/s] | 4.731×10-3 | 9.636×10-3 |
| Outp(P1-P2)[m/s] | 8.772×10-4 | 3.545×10-4 |
| ∆P(Pa) | 4.594×106 | 7.773×106 |
Conclusions
다이 형상 최적화에 사용된 평판 다이는 James Allen의 연구에서 최초의 해석 결과 출구 속도 분포가 균일하지 않아 논문에서는 In-Equality penalty 알고리즘과 Equality penalty 알고리즘을 이용하여 최적화하였다. 본 논문은 James Allen의 논문과 동일한 알고리즘을 사용하지 않고 최적화 프로그램 중 상용 소프트웨어인 Ansys DesignXplorer를 사용하였다. 최적화에서 첫 번째 실험 설계에서 중앙 복합 디자인(Central composite design) 모델을 사용하였다. 응답 표면에서는 Kriging 모델 사용하였고 최적화에는 응답 표면 최적화(Response surface optimization)을 선택하였다.
실험 설계에서는 다이의 형상 변경 부분을 설정하고 최대값과 최소값을 선택하여야 하므로 매니폴더의 최소 길이는 54 mm, 최대 길이는 90으로 설정하였으며 랜드의 길이는 최소 2 mm에서 최대 7 mm로 랜드의 두께를 최소 8 mm에서 최대 48 mm로 설정하였다. 위의 값으로 설정하게 되면 최소 값과 최대 값에 따라 임의의 실험 설계 포인트를 설정하여 해석을 진행하게 된다. 다음 단계인 응답 면은 실험 설계의 값을 바탕으로 다이 형상 변경에 따른 목적함수의 근사 값들의 데이터를 그래프로 나타낸다. 최적화는 응답 표면의 근사 값을 바탕으로 원하는 최적 설계를 진행하기 위해 제약 조건을 설정하게 된다.
본 논문에서는 “Outp”는 0 m/s에 가까운 값, 압력은 8×106 Pa 보다 낮은 압력을 검색하도록 제약 조건을 설정하였다. 본 논문에서는 “Outp”의 편차가 가장 작고 압력이 7.5×106 Pa 정도인 값을 검증 값으로 설정하였다. 본 논문에서 최적화 시 고려하지 못한 것은 압출물의 두께이다. 두께는 압출 공정에서 중요한 부분 중 하나이다. 하지만 압출물의 두께는 압출 공정 이후 필름 캐스팅(Casting) 공정에서 제어가 가능하기 때문에 압출물의 두께 보다 출구 속도의 균일성에 중점을 두고 최적화를 진행하였다. 최종적으로 다이 출구의 속도가 증가하여 압출물의 토출량이 증가하였으며 “Outp”의 값은 현저히 줄어들었다. 압력 구배 또한 실제 공정 조건과 비슷하기 때문에 압출물의 균일성 부분에서는 최적화가 완료되었다.