A Study on Transformation of Dynamic DSC Results into Isothermal Data for the Formation Kinetics of a PU Elastomer

Introduction

우레탄 반응은 –NCO 관능기인 이소시아네이트(Isocyanate)가 반응성이 매우 높기 때문에 핵친화성 물질들인 –OH 및 –NH 등의 관능기를 가진 화합물과 반응하여, 우레탄 (Urethane), 우레아(Urea), 알로파네이트(Allophanate), 비우렛 (Biuret) 반응 등의 매우 복잡한 반응기구를 통하여 다양한 폴리우레탄 화합물을 생성하게 된다.¹ 폴리우레탄 탄성체 (Urethane Elastomer)는 하드 세그먼트(hard segment)와 소프트 세그먼트(soft segment)의 블록공중합체로 이루어지는데, 낮은 유리전이온도(T_g)를 가지는 소프트 세그먼트는 일반적으로 분자량 400~5,000 정도의 폴리에테르 폴리올 또는 폴리에스테르 폴리올로 부터 만들어지며 폴리우레탄 탄성체의 신율 및 탄성율에 영향을 미치게 되고, 이소시아네이트와 쇄연장제로부터 형성되어 딱딱하고 높은 T_g를 가지는 하드 세그먼트는 폴리우레탄 탄성체의 기계적 물성에 영향을 미치게 된다.²

폴리우레탄 탄성체를 제조하는 법은 전통적으로 원샷 (One-shot) 방식이나 프리폴리머 방법 중의 한 가지 방법으로 만들어 진다. 원샷 방식은 폴리올과 이소시아네이트, 쇄연장제, 촉매 등의 모든 재료들을 한꺼번에 혼합하여 반응시키는 방법으로서 반응조절이 어려운 대신에 가장 쉽고 빠르게 제품을 만들 수 있어 경제적인 측면에서 유리한 면이 있다. 이와는 달리 프리폴리머 방식은 화학 반응의 기구나 최종 제품의 구조나 열적 기계적인 물성 등을 매우 미세하게 조정하는 것이 용이하기 때문에 수요자 맞춤형의 일반적 제품이나 고성능 코팅 및 페인트 등의 분야에서 일반적으로 많이 사용되는 기술이다.^3,4 이에 따라 폴리우레탄 반응에서의 반응기구 및 속도론을 자세히 이해하는 것은 제품의 물성 조절을 위하여 필수적인 사항이라 할 수 있다.

우레탄 반응의 반응기구 및 속도론에 대한 연구는 GPC, FTIR, DSC 및 TGA 등의 기기분석적인 방법을 이용하여 다양하게 연구되고 있으나, 우레탄 반응의 반응 속도가 매우 빠른 경우가 많기 때문에 많은 제약 조건이 따르게 된다.^5-8 또한 폴리우레탄 반응이 우레탄, 우레아, 알로파네이트 (Allophanate), 비우렛(Biurete) 반응 등의 매우 복잡한 반응기구를 포함하고 있으므로 현재까지도 그 반응기구에 대하여 많은 연구가 진행되고 있다.

DSC (Differential Scanning Calorimetry) 열분석법에서의 등온(Isothermal) 또는 비등온(Non-isothermal) 방법을 이용하는 반응속도론에 관한 연구는 DSC 실험의 편의성과 데이터 해석의 용이성 등에 힘입어 수 많은 연구가 이루어져 왔으며, 그 연구결과의 타당성 및 적용가능성이 입증되고 있다.⁹ 그러나, 등온실험에서는 일정온도에서의 시간에 따른 열량변화를 측정하므로, 측정된 데이터를 해석하기가 매우 쉬운 장점이 있으나, 정해진 특정 온도에 도달하기 위한 시간에 따르는 실험적 문제점으로 인하여 반응 초기 부분의 정보 획득에 대한 어려움이 있고, 일정 온도에 이르기까지의 급격한 가열에 의한 시료의 팽창 등에 의하여 재현성 있는 결과를 얻기 어려운 난점 등이 여전히 존재하고 있다. 비등온 실험은 일정한 승온율에서 온도 변화에 따른 열량변화를 측정하게 되므로 이러한 문제점을 해결할 수 있고, 실험이 간단하기 때문에 대개의 경우 비등온 실험 방법을 선호하고 있으나, 측정된 데이터의 해석이 상대적으로 어려운 점 등의 문제점이 있다. 여러 가지 모델식을 이용하는 방법들이 제안되어 있으나, 고분자 가교반응에서의 활성화 에너지는 일반적으로 반응의 진행 정도에 따라서 변화하게 되며 어떤 kinetics 모델을 적용하여 계산했느냐에 따라서도 달라지게 된다. 따라서 이를 해결하기 위한 많은 연구가 진행되었으며, 현재까지 알려진 비등온 데이터를 이용하는 많은 반응속도론(reaction kinetics)의 연구 방법 중에서도 등전환율 방법(Isoconversional method)은 전환율에 따른 반응속도론의 변화를 반영해 줄 수 있기 때문에 가장 정확성 있는 방법으로 알려져 있다.^10,11 등전환율 방법 중에서도 Arrhenius 법칙을 따른 등온실험과 비등온 실험의 Ozawa해석법이 제일 신빙성 있는 결과를 얻을 수 있는 것으로 알려져 있다. 따라서 비등온 실험의 Ozawa 해석법은 Arrhenius 법칙을 따른 등온 실험의 결과로 변환될 수 있으며 이들의 상관관계와 동등성에 대한 많은 연구가 진행된 바 있다.^12,13

본 연구에서는 PTMG/TDI 타입의 이소시아네이트 프리폴리머와 활성수소를 가진 아민화합물인 MOCA와의 반응에 대하여 Dynamic DSC를 이용하여 열분석 곡선을 얻은 다음, 이로부터 등전환율 방법을 적용하는 Ozawa의 해석방법에 기반한 등온 데이터로의 변환 방법을 알아보고 이로부터 폴리우레탄 엘라스토머의 생성 반응에 대한 반응기구를 해석하여 보고자 하였다.

Experimental

실험에 사용된 이소시아네이트 프리폴리머는 ㈜동성화학의 DSE-195P를 사용하였다. DSE-195P는 Toluene diisocyanate (TDI)와 Poly(tetramethylene ether glycol) (PTMG)의 반응에 의하여 만들어지는 PTMG/TDI 프리폴리머로서 NCO% 6.6 ± 0.1 정도의 이소시아네이트 관능기를 가지고 있다. 쇄연장제 및 경화제로 사용되는 MOCA는 4,4'-methylene-bis(2-chloroaniline)의 상품명으로서 분자량 267.15 g/mol이며 두 개의 아민 관능기를 가진다.

Dynamic DSC 실험은 Perkin Elmer DSC-7 Differential Scanning Calorimeter를 사용하여 질소분위기에서 7, 5, 3, 및 1°C/min의 서로 다른 승온속도로 상온에서 180°C 까지 승온시키면서 온도변화에 따른 열량변화 곡선을 얻었다. 샘플은 당량비로 정량된 MOCA를 120°C에서 녹인 후에 이소시아네이트 프리폴리머(DSE-195P)에 투입하면서 빠르게 교반하면서 상온으로 냉각하여 실험 전 반응이 일어나는 것을 최소화하였다. 열분석에 필요한 샘플은 약 10 mg으로 하고 각각의 승온율에서의 전환율(α)은 전체 peak 면적에 대한 각각의 온도에서의 상대적인 면적비로 계산하였다.

Results and Discussion

일반적인 화학반응에서의 반응속도식은 다음의 식 (1)로 표현될 수 있다.

여기서, k 는 속도상수로 절대온도, T의 함수이며 식 (2)에서와 같이 아레니우스 유형으로 표시된다.

k_o : frequency factor

E_a : 활성화 에너지

R : 가스 상수

한편 전환율의 함수 f(α)는 반응의 형태에 따라 여러 가지 형태의 함수로 표시되는데, 고분자 축중합반응에서와 같이 반응생성물이 반응속도에 영향을 미치는 경우에는 식 (2)에서와 같이 자촉매반응(autocatalytic reaction) 모델이 더 적합한 것으로 알려져 있다.^14,15

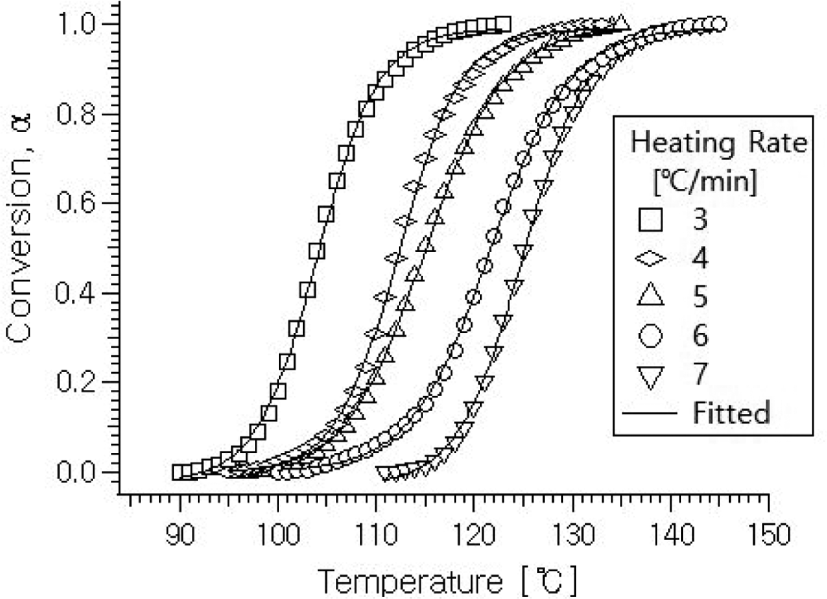
Figure 1에는 여러 가지 서로 다른 승온속도에 대한 DSC 열분석 곡선을 나타낸다. 그림에서 보아 잘 알 수 있듯이 본 연구 시스템에서의 폴리우레아 생성반응은 발열 반응으로서 전환율 0.5 정도에서의 최고반응이 일어나는 피크 점의 온도는 100~130°C의 온도 범위이며 승온속도가 빨라질수록 샘플의 열평형에 이르는 온도가 더 높아지게 되므로 반응에 의한 발열 피크는 점점 더 높은 온도로 이동해가는 것을 알 수 있다. 또 다른 한 가지는 1°C/min 작은 승온속도 차이에 따라서도 피크의 이동현상이 심한 것으로 볼 때, 이 반응이 온도 변화에 대하여 매우 민감한 반응임을 알 수 있다.

Figure 1. DSC thermograms of DSE-195P/ MOCA system with β = 3, 4, 5, 6, and 7°C/min.¹⁶

Download Original Figure

비등온 DSC 결과의 등온 데이터 변환

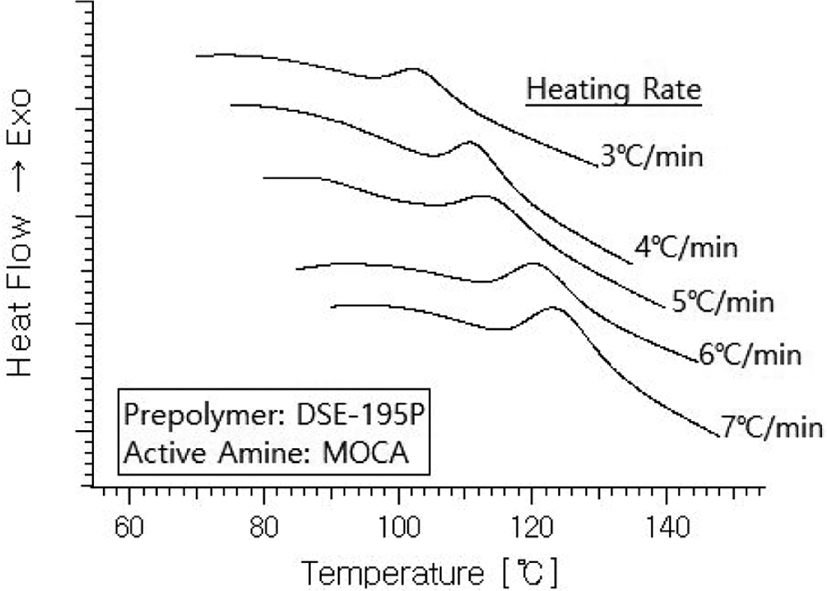
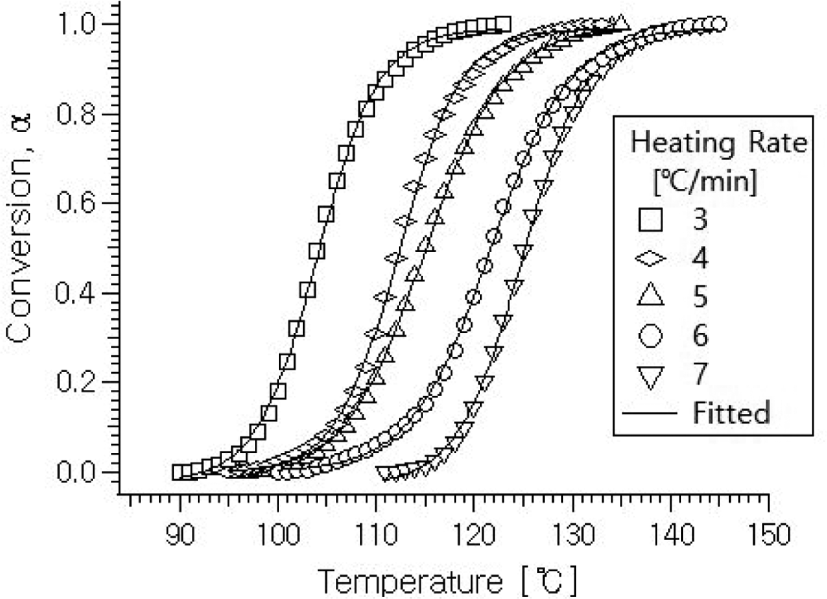
Figure 1에서의 그림으로부터 각 승온속도에서의 온도에 따른 전환율 α는 생성반응 전체 피크 면적에 대한 각 온도에서의 면적비로 정의되므로 각각의 승온속도에서의 온도에 따른 전환율을 구하여 플롯해 보면 Figure 2에서 보이는 바와 같다.

Figure 2. α-T plot at each constant heating rate calculated from Figure 1.

Download Original Figure

한편 전술한 바와 같이 DSC를 이용하는 비등온 실험은 실험이 간단하면서도 비등온 실험에서는 어려운 고온에 이르기까지 스캔이 가능하므로 비등온 실험 데이터를 등온 변환하여 손쉬운 해석을 통하여, 비등온 DSC의 결과와 등온 실험의 데이터를 연관시켜 해석하는 일은 반응 모델의 확인 비교에 많은 도움이 될 수 있다.

다음에 Figure 2의 그림으로부터의 비등온 실험 결과를 등온 데이터로의 변환에 의하여, 일정 온도에서의 동일 전환율에 이르는 시간에 관한 데이터는 다음의 순서에 따라 작성할 수 있다.

1. Figure 2의 그림에서 Figure 3에서 예시한 바와 같이 y축의 일정 전환율에서 수평선을 긋는다.

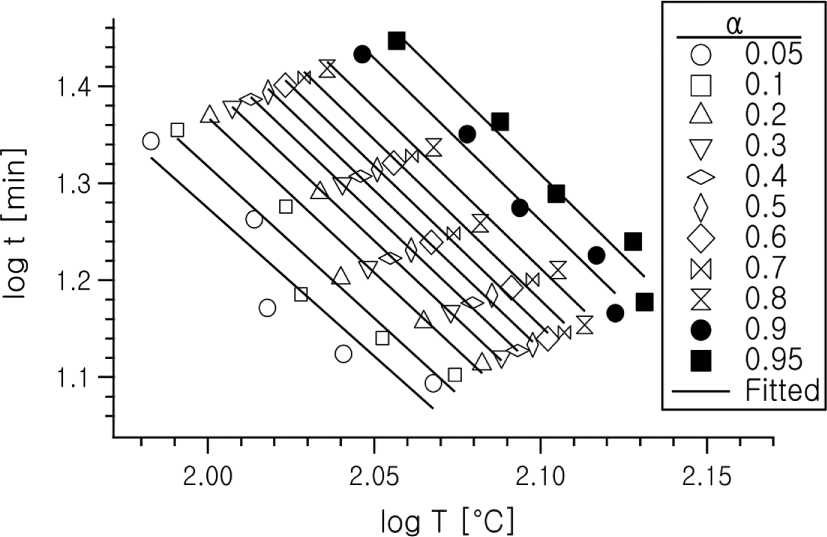
2. 수평선이 일정 승온율 곡선과 만나는 각 점에서의 x축 온도를 읽고, t=(T−T_o)/β 의 수식을 이용하여 (logt−logT)_α다이아그램을 작성한다. 예를 들어 α=0.4 인 전환율에서 수평선 그으면, β=3 및 7인 곡선과 만나는 점의 온도는 각각 T₁ = 102°C 및 T₅=125°C가 되고 이 온도에 이르는 시간은 T_o 가 30°C인 경우에,

   $$\begin{array}{l}{t}_1=(T_1-T_0)/\beta =(102-30)/3=24\text{}\text{}\text{}\min \\ t_5=(T_5-T_0)/\beta =(125-30)/3=31.7\text{}\text{}\min \end{array}$$
   이 된다. 이와 같이하여 각각의 일정 전환율에서의 (t, T) 세트를 만들면 (logt−logT)_α 다이어그램을 만들 수 있다.

3. 전환율 0.05–0.95 사이의 여러 가지 일정 전환율에 대하여 (logt-logT)_α 를 작성한 그림을 Figure 4에 나타내었다.

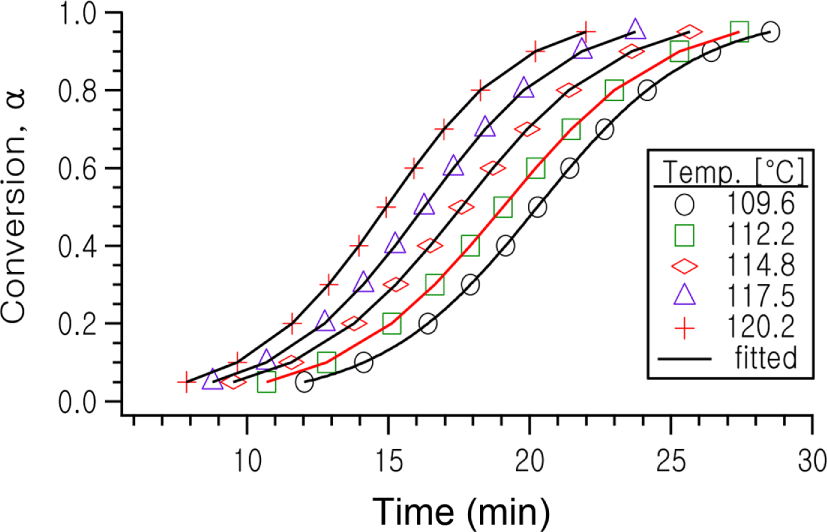
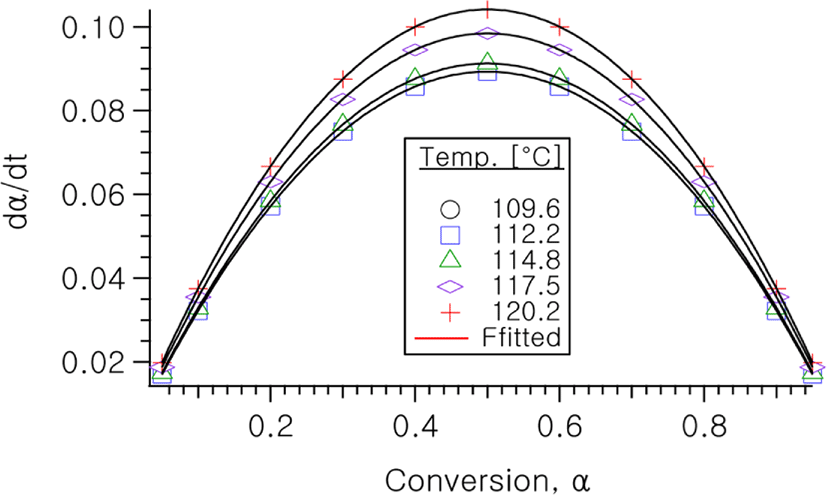
4. Figure 4에서 등온 실험을 행할 경우의 원하는 일정 온도를 x축에서 정하여 수직선을 그으면 (α, t) 세트를 작성할 수 있고, 이로부터 일정온도에서의 시간에 따르는 전환율, (α−t)_T 커브를 얻을 수 있게 된다. Figure 5에는 이렇게 하여 얻어진(α−t)_T plot을 나타내었다. 또한 이로부터 도출되는 dα/dt vs. α plot을 나타내었다.

Figure 3. Schematic representations for the isoconversional (logt − logT)_α plot.

Download Original Figure

Figure 4. Isoconversional (logt − logT)_α plot from the dynamic DSC results.

Download Original Figure

Figure 5. (α−t)_T plot transformed from dynamic DSC data.

Download Original Figure

이 그림들로부터 보이는 전형적인 sigmoid type과 전환율에 따른 반응속도의 변화 형태는 이 반응이 자동촉매 반응기구를 잘 따르고 있음을 보이는 것이다.

한편 이렇게 도출된 등온 실험 데이터를 이용하면 식 (3)에서의 자동 촉매 반응 모델을 이용하는 경우의 반응속도 매개변수(kinetic parameter) 들을 쉽게 계산할 수 있다.

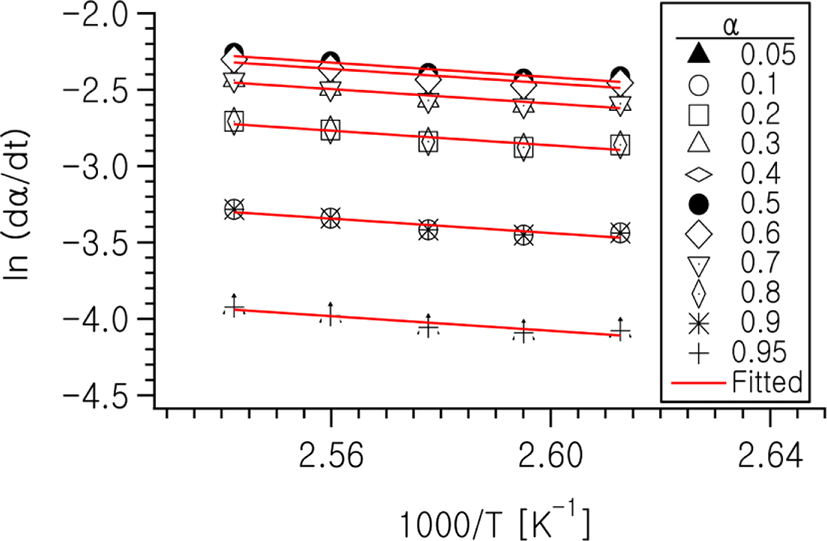
식 (1)의 양변에 로그를 취하면 식 (4)에서와 같이 표현 되므로 Friedman의 해석방법에 따라 일정 전환율에서의 $\ln \frac{d\alpha }{dt}vs.\frac{1}{T}$ 를 플롯하면 기울기로부터 활성화 에너지를 구할 수 있다.

$$\ln \frac{d\alpha }{dt}=\ln \text{}Af(\alpha )-\frac{E_a}{RT}$$

(4)

Figure 7에는 각 전환율에서의 $\ln \frac{d\alpha }{dt}vs.\frac{1}{T}$ 플롯한 결과를 나타낸다. 그림에서 보듯이 전체 전환율 영역에 걸쳐 일정한 기울기 값을 보여주고 있고, 이로부터 계산된 활성화 에너지 값은 약 20.0 kJ/mol로 계산되었다.

Figure 6. (dα/dt−α)_T plot calculated from Figure 5.

Download Original Figure

Figure 7. Friedman plot of $\ln \frac{d\alpha }{dt}vs.\frac{1}{T}$ at constant conversion

Download Original Figure

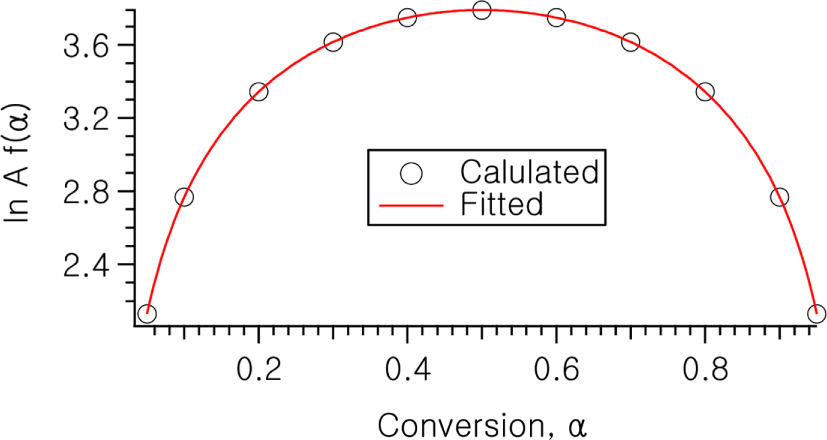
한편 $\ln \frac{d\alpha }{dt}vs.\frac{1}{T}$ 의 절편값 ln Af(α)는 전환율 α의 함수이고, 이는 식 (3)에서와 같이 α^m(1-α)ⁿ 의 자동촉매 반응식의 형태로 나타낼 수 있다. Figure 8에는 $\ln \frac{d\alpha }{dt}$ 을 전환율 α의 함 수로 나타낸 것이다. 이 그림으로부터 계산되는 A, m, n 은 각각 A=e^5.2, m=n=1.0으로 나타났다. 이러한 결과는 같은 시스템에 대한 비등온 실험 결과로 부터 도출되었던 결과와 같이 이 반응이 전형적인 자동촉매 반응를 잘 따른 다는 것을 나타낸다.¹⁶

Figure 8. ln Af(α) vs α of Friedman plot.

Download Original Figure

따라서 지금까지의 결과를 종합하여 보면, 본 연구의 DSE-195P/MOCA 시스템에 대한 반응속도식은 다음의 식 (5)에서와 같이 나타낼 수 있다.

$$\begin{array}{l}\frac{d\alpha }{dt}=A\text{}\text{}\text{}\text{}\exp \left(-\frac{E_a}{RT}\right){\alpha }^m{\left(1-\alpha \right)}^n\hfill \\ \text{}\text{}\text{}\text{}=e^{5.2}\text{}\exp \left(-\frac{20,000}{RT}\right)\alpha (1-\alpha )\hfill \end{array}$$

(5)

Conclusion

주어진 MOCA와 이소시아네이트 프리폴리머와의 중합반응에 대하여 Dynamic DSC 법을 이용하여 서로 다른 승온속도에서의 열분석 곡선을 얻고 이로부터 순차적인 과정을 거쳐 등온데이터로 전환할 수 있었다. 연구를 통하여 다음의 결과를 얻을 수 있었다.