Particle-based Numerical Modeling of Linear Viscoelastic Materials using MPM based on FEM for Taylor Impact Simulations

Introduction

입자기반 해석 모델은 크게 SPH (smoothed particle hydro-dynamics),¹ DEM (discrete element method),² MPM (material point method),³ HPEM (hybrid particle element method)⁴ 등으로 크게 나누어 진다. 이중에서 본 연구에서 사용하고자 하는 MPM (Material Point Method)은 물체를 고정된 계산 격자(grid)와 라그랑지안 질점(Lagrangian material point)으로 나타내는 방법이다. 계산 격자는 공간에 고정되거나 필요에 따라 적절히 바뀔 수 있게 정할 수 있다.

라그랑지안 질점은 물체의 변형에 따라 이동하기 때문에 경로 의존적인 변수로 표현되는 구성방정식에 적용하기 쉽다. 또한 MPM에서 사용하는 질점과 FEM에서 사용하는 고정 격자 사이의 적절한 변환을 통하여 라그랑지안과 오일러리안의 장점을 취할 수 있는 방법이 MPM이며 개발 초기부터 유체 동역학 문제에 많이 적용되었다. 고속 충돌, 폭발과 같은 국방과학 연구 분야나, 복합 재료의 혼합에 이용되는 입상 재료(granular material)의 유동 해석과 같이 대변형 문제에도 많은 적용이 이루어 졌다.⁵

고 변형률 속도 조건에서의 고분자 변형은 보호 차폐 및 보호 장치와 같은 내 충격성 응용 분야에서 고려해야 할 주요 요인이다. 테일러 충격 시험은 이에 대한 기초 실험으로 연구가 진행되었으며 재료 특성에 따라 로드의 변형 특성을 찾기 위한 많은 이론적 및 실험적 연구의 주제가 되어 왔다.⁶ 테일러 충격 시험에서 원통형로드는 단단한 플레이트에 상대적으로 높은 속도로 충돌되어 짧은 시간 경과 후에 상당한 영구 변형과 리바운드를 생성한다. 점탄성 재료에 관한 한 충격시의 변형 특성은 일반적인 탄성 재료에 비해 상당히 다르다. 본 연구자에 의해 강성 플레이트에 영향을 미치는 점탄성 물성을 가진 테일러 충격 실험에 대한 실험과 수치해석 결과가 보고되었다.^7,8 본 연구에서는 PE, PC, PEEK와 같은 고분자 재료의 변형 및 파괴 거동을 고속 사진 촬영을 통한 Taylor 실린더 충격 시험으로 조사하였다. 충격 실험을 수행하기 위해 20 mm 공기총이 사용 되었고, 충격 실험 후 발사체의 모양을 검사하고 사진 이미지와 비교하여 탄성 변형 구성 요소를 순간적으로 측정된 변형과 구별하였다. 또한 점탄성 효과를 분석하기 위해, FEM 수치 해석을 수행하였고, 고분자 재료는 완화 시간 및 전단 계수와 점탄성 구성 관계를 사용하여 모델링 하였고, 충돌시 고분자 막대의 변형에 대한 점탄성 감쇠 상수의 효과를 논의하였다.

본 연구에서는 선형 점탄성 재료에 대하여, FEM 해석을 기반으로 한 입자 기반 충돌, 대 변형으로 인한 파괴 등에 응용하기 위해 MPM 수치 방법을 도입하였다.⁹ X. Zhang 그룹은 MPM에 대한 방대한 논문과 관련 서적을 저술하였으며 자세한 이론적 배경과 응용 예에 대해서는 이 서적을 참조하였다.⁹ 이를 바탕으로 본 연구에서는 FEM 수치 해석 기법을 기본으로 하여, 점탄성 재료의 입자 기반 해석 모델 수립 및 프로그램 개발을 수행하고자 한다. 이를 위해 MPM 수치 해석 기법을 적용하고이를 점탄성 봉에 대한 테일러 충격 시험에 도입하여 FEM 결과와 비교하여 본 연구에서 구현한 선형 점탄성 입자 기반 MPM 프로그램 해석 결과를 검증하고 분석하고자 한다.

Governing Equations

일반적으로 고체 변형 해석에서의 연속 방정식, 운동량 방정식은,

여기에서 ρ는 현재의 밀도(density), ρ₀, F 는 변형 전 밀도와 변형구배(deformation gradient) 텐서, J 는 야코비안(Jacobian)ẍ, $\ddot{y},\ddot{z}$ 는 x, y, z 방향의 가속도, σ 는 전 응력(total stress) 텐서이다.

MPM based on FEM for Linear Viscoelastic Models

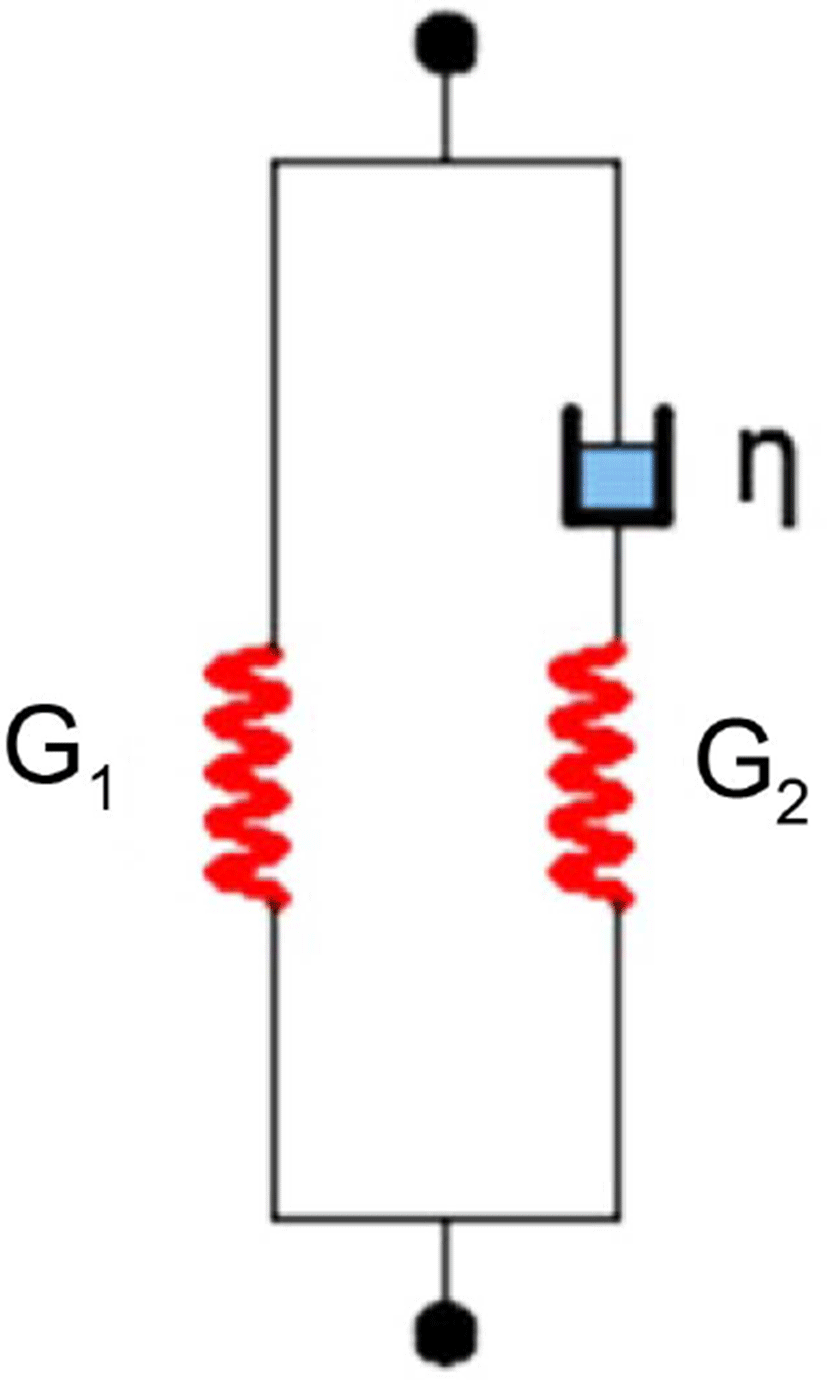
점탄성 고체에서 선형 점탄성 모델을 적용하면, 완화 전단계수(relaxation shear modulus)는 Figure 1에 나타난 것과 같이 스프링과 감쇠가 병렬로 연결되며 이를 식으로 나타내면 아래와 같이 표현된다.^10,11,12

Figure 1. Linear viscoelastic solid model.

Download Original Figure

식에서 G₀ 는 short-time 전단계수, G_∞는 long-time 전단계수, β 는 감쇠상수(decay constant)이다. 감쇠계수는 완화시간 의 역수이며 Figure 1에 나타낸 것처럼 $\beta =\frac{G_2}{\eta }$ 로 표현된다. 시간 스텝 n에서 편차응력 텐서는 다음과 같이 편차 탄성 응력 텐서와 편차 점탄성 응력 텐서의 합으로 구해질 수 있다.

$S_{e,ij}^n$ 는 long-time 전단 계수와 Bulk modulus K 을 이용하여 구해진다. 시간 t_n 에서 편차 점탄성 응력 텐서는 아래와 같이 정의된다.

여기서 완화 전단 계수 G_v(t)는 아래와 같다.

위와 같은 편차 점탄성 응력 텐서를 차분화하여 시간 증분에 따른 새로운 응력을 구하기 위한 최종 공식은 다음과 같이 표현된다.

선형 점탄성 모델의 구현은 $S_{ij}^n=S_{e,ij}^n+S_{v,ij}^n$ 을 계산하여 구할 수 있다. 이를 MPM 코드에 구현 하였다.

여기서 일반적으로 테일러 충돌처럼 물체가 충돌 전, 후 회전이 포함되어 있다면, FEM에서 응력 갱신은 다음과 같다.^11,12 즉, 구성 방정식상에서 요소의 회전 효과를 고려하기 위해서 일반적으로 Jaumann rate이 사용된다. 편차응력에 Jaumann rate을 사용하면 스핀 텐서(spin tensor)(W)로 표현된다.^11,12

응력 상태는 외연적 방법(explicit method)으로 계산되기 때문에 때로는 항복 조건을 만족하지 않는 경우가 발생하며, 이를 방지하기 위해 본 연구에서 반경 회기법(radial return method)을 사용하였다.^11,12

이러한 FEM을 바탕으로 MPM 은 입자 기반 해석 방법 중 하나로 공간적으로 다양한 필드(예: 변위, 속도, 응력 등)를 묘사할 수 있는 FEM 격자를 사용한다. 즉 전체적으로 FEM 공식화와 유사하지만 고정 FEM 격자(grid)를 사용하므로 대 변형의 경우 격자의 변형을 신경 쓰지 않아도 되는 장점 때문에 최근 고속 충돌 및 대 폭발 해석을 위해 정밀한 알고리즘 개발이 시도되고 있다. 중요 해석 과정은 다음과 같다.

MPM은 FEM 그리드에 겹쳐 있는 질점(material point)에 필드 값을 저장한다. MPM 질점에 저장된 필드 값들은 FEM 고정 격자 위로 매핑이 되며 이로부터 운동 방정식을 풀고 여기에서 가속도 필드를 고정 격자에서 업데이트하게 된다. 그런 다음 표준 FEM 필드 매핑 방법을 이용하여 질점 값을 업데이트하는 데 사용되며 FEM 격자가 그대로 유지하거나 간단한 다른 FEM 격자로 다시 재조정 될 수 있으며 자세한 내용은 참고 서적을 참조하였다.⁹

Results and Discussion

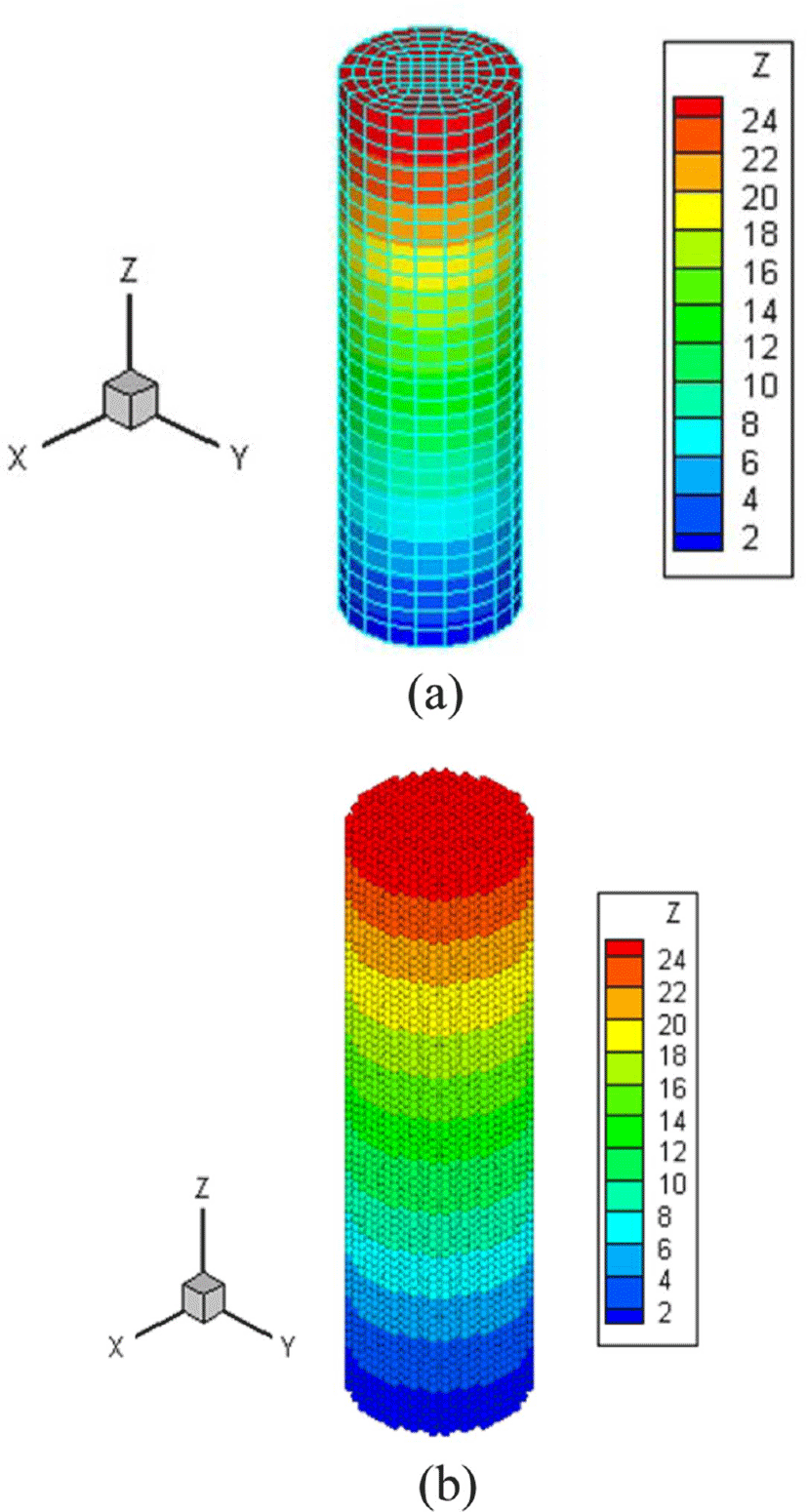
FEM을 기초로 구현된 선형 점탄성 해석용 MPM 프로그램을 검증하기 위하여 FEM 해석 및 MPM 해석, 두 가지 방법으로 전산 수치 해석을 수행하였다. 수치 시뮬레이션은 단시간 및 장시간 전단 계수, 감쇠 상수 및 체적 탄성 계수와 같은 점탄성 물질 상수를 MPM에 적용하여 수행되었다. 점탄성 테일러 실험용 막대의 반지름은 3.8(mm)이고 길이는 25.4 (mm) 이다. 초기 충돌 속도는 150(m/s) 이다. 충돌면은 Figure 2에 나낸 것처럼 충돌봉 하단 면에서 0.01(mm) 아래로 충돌봉과 수직한 무한 평면으로 설정하였다. Figure 2는 점탄성 해석에서 3D Taylor 충격 시험을 위한 초기 FEM 메쉬와 MPM 입자 질점 분포를 나타낸다.

Figure 2. (a) Element meshes for FEM and (b) material particles for MPM.

Download Original Figure

Figure 2에서와 같이, MPM 입자는 21,172개로 하였고 분산된 입자는 충돌 파괴에 의해 외부로 나갈 수 있도록 설정하였다. 고정 격자는 x방향으로 −6.5(mm)에서 6.5(mm) 로, y방향으로 −6.5(mm)에서 6.5(mm) 로, z방향으로 −0.01(mm)에서 26.5(mm)로, 설정하였고 정육면체 격자 하나의 길이는 0.5(mm)로 설정하였다. FEM의 경우는 3차원 유한 요소 형상은 원주를 따라 가면서 정확하게 매핑이 되지만 MPM의 경우에서는 완벽하게 매핑 되기 어렵다. 이를 위하여는 입자의 질점 분포를 원주를 따라가면서 분포시켜야 하고 각 입자가 가지는 질량도 균일하지 않으므로 FEM 형상 함수를 도입하여 재 설정하여야 하지만 본 연구에서는 균일한 입자 분포로 배열 하였으므로 모든 입자가 가지는 질량을 동일하게 적용하였다.

수치 해석에 사용된 봉의 재질은 고분자 재료 PE에 해당하게 설정하였다. 즉, 밀도, 체적 탄성 계수, 단시간 및 장시간 전단 계수, 감쇠 상수를 각각 1.0(g/cm³), 0.14(GPa), 550(GPa), 5(MPa), $650\left(\frac{1}{\mu s}\right)$ 를 사용하였으며, 이를 사용하여 FEM으로 해석하였다. 실험과 수치해석 결과 비교 및 분석에 대한 자세한 연구는 다음 논문에서 논의 할 예정이다. 이 결과를 Figure 3(a) Time = 5.0(μs) (b) Time = 10.0(μs) (c) Time = 20.0(μs)의 세가지 시간 경과에 대하여 높이 변화를 나타내었다. 여기서 알 수 있듯이 150(m/s) 속도로 충돌할 경우 선형 점탄성 모델에 의해 충돌면에서 버섯 모양의 점성 변형이 발견되고 있다.

Figure 3. Figure 3. (a) Time = 5.0(μs) (b) Time = 10.0(μs) (c) Time = 20.0 (μs) for FEM.

Download Original Figure

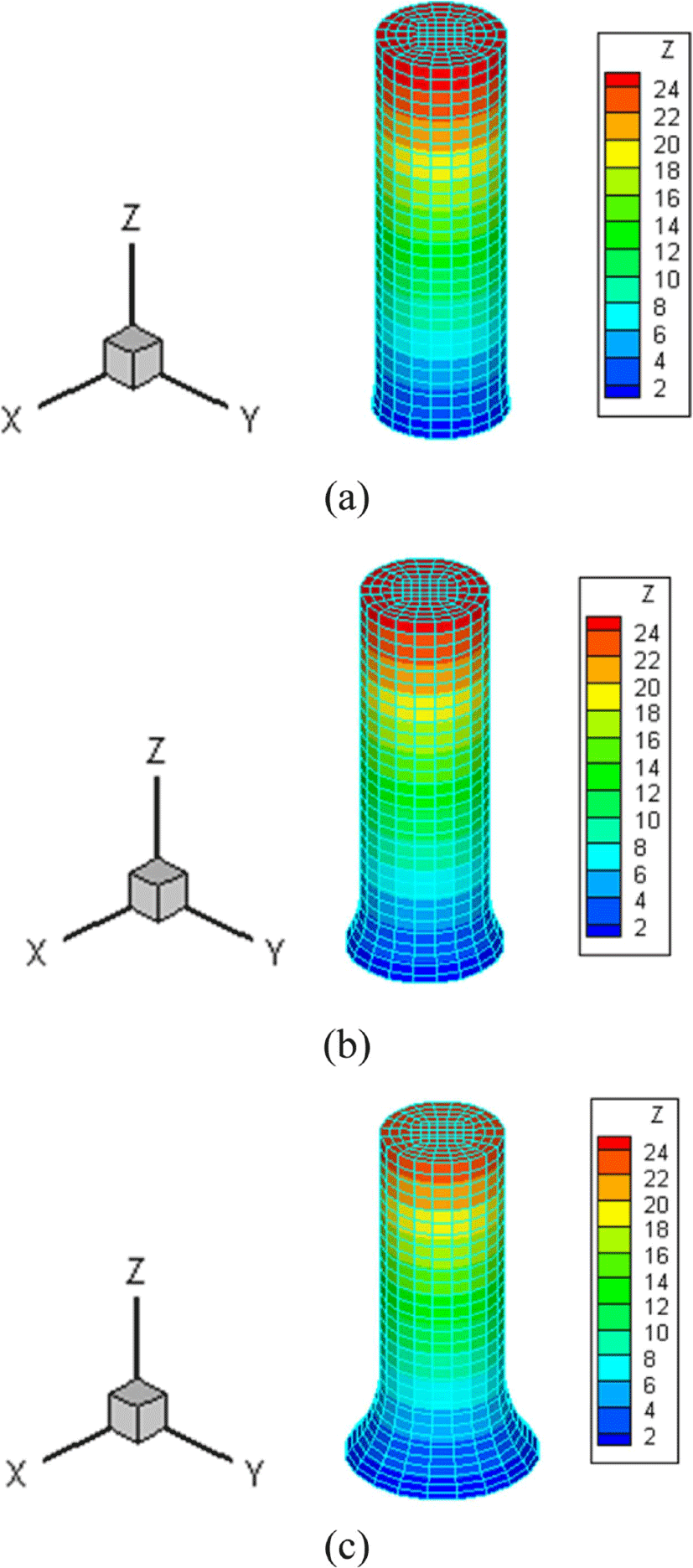
동일한 조건에서 MPM으로 해석한 결과를 Figure 4에 나타내었다. Figure 3과 Figure 4를 각각 비교하여 보면 FEM과 MPM의 두 경우 일치한 수치 결과를 얻을 있었다. 이로부터 유한 요소 법으로부터 입자 질점으로 변환한 MPM 모델링의 수치 결과가 양호함을 검증할 수 있었다.

Figure 4. (a) Time = 5.0(μs) (b) Time = 10.0(μs) (c) Time = 20.0 (μs) for MPM.

Download Original Figure

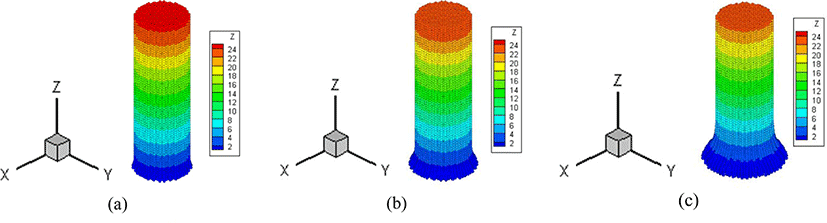
밀도, 체적 탄성 계수, 단시간 및 장시간 전단 계수를 각각 1.0(g/cm³), 0.14(GPa), 550(GPa), 5(MPa)을 고정하고 감쇠 상 수를 6.5, 65, $650\left(\frac{1}{\mu s}\right)$ 으로 각각 사용하여 FEM과 MPM으로 각각 해석한 결과를 Figure 5에 나타내었다. 감쇠상수의 값이 $6.5\left(\frac{1}{\mu s}\right)$ 일 때는 육안으로 형상의 차이를 구분하기 어려우나, 65, $650\left(\frac{1}{\mu s}\right)$ 일때는 그 차이를 확연히 구분할 수 있을 정 로 점성에 의한 변형이 증가 함을 알 수 있다. 감쇠 상수는 완화 시간의 역수이므로 감쇠 상수가 클수록 완화 전단 계수(relaxation shear modulus)는 G_∞값으로 빠르게 수렴하게 되어 재료의 응력이 감소하게 된다. 이와 같은 이유로 감쇠 상수가 충격 속도를 이기지 못하고 충격부분에서 변형이 크게 발생하게 됨을 알 수 있다. 또한 FEM과 MPM의 두 경우 충격 부위의 변형 정도가 유사한 수치 결과를 얻을 있었다. 이로부터 입자 질점으로 변환한 MPM에 대한 프로그램 구현 및 모델링의 수치 결과 검증은 일관성 있는 좋은 결과를 얻을 수 있었다.

Figure 5. Decay constant = $6.5\left(\frac{1}{\text{μ}s}\right)$ , $65\left(\frac{1}{\text{μ}s}\right)$, and $650\left(\frac{1}{\text{μ}s}\right)$ from left to right at time = 20.0 (μs) (a) for FEM and (b) for MPM.

Download Original Figure

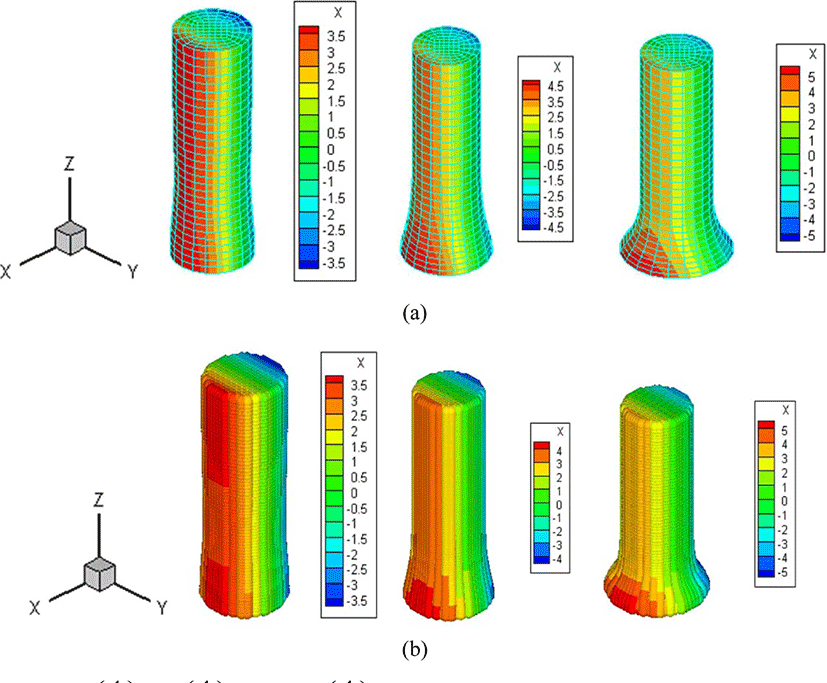
Figure 5와 같은 조건, 즉 밀도, 체적 탄성 계수, 단시간 및 장시간 전단 계수를 각각 1.0(g/cm³), 0.14(GPa), 550(GPa), 5(MPa)을 고정하고 감쇠 상수를 6.5, 65, $650\left(\frac{1}{\mu s}\right)$ 으로 각각 사용하여 MPM으로 해석한 결과를 수직방향의 충돌 속도로 Figure 6에 나타내었다.

Figure 6. (a) β = 6.5(1/μs) (b) β = 65(1/μs) (c) β = 650(1/μs) at time = 20.0(μs) for MPM at time = 20(μs).

Download Original Figure

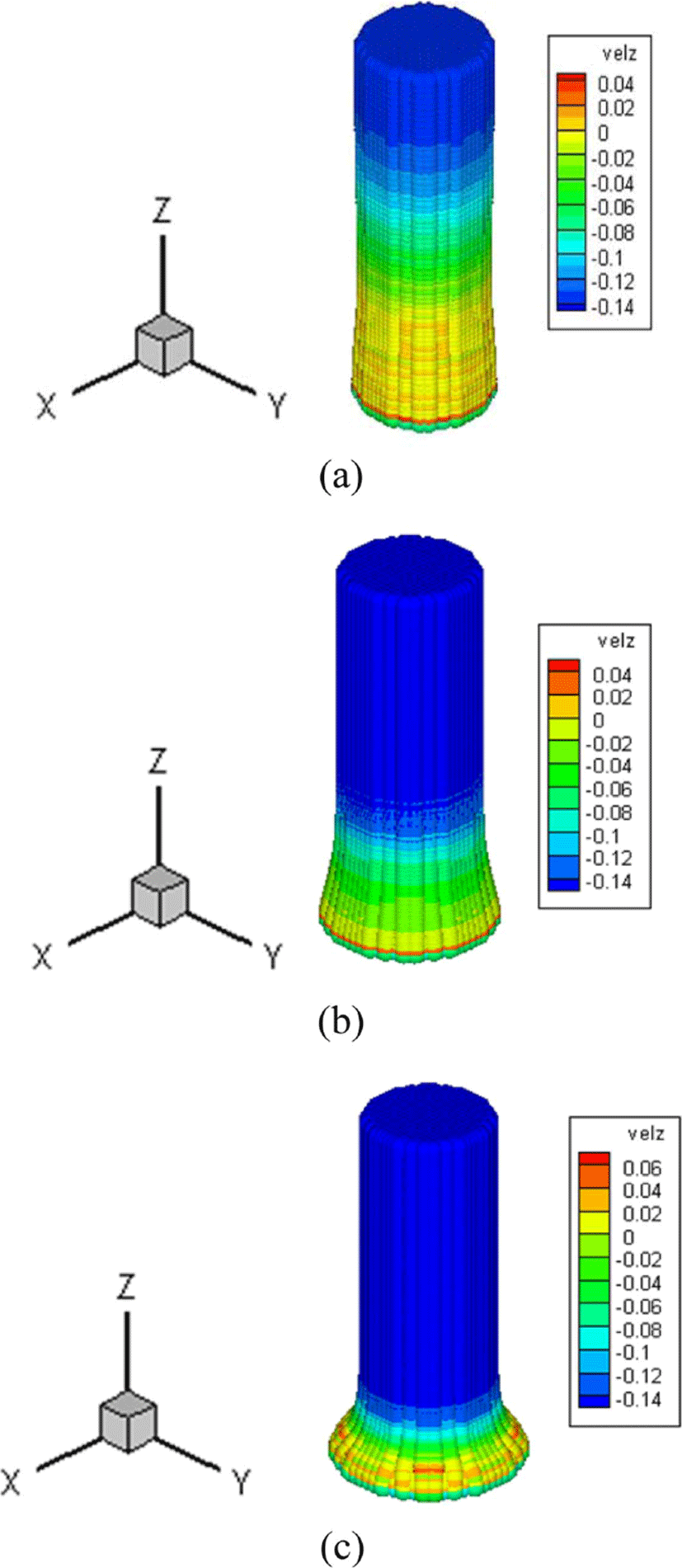
이 수치 결과로부터 감쇠 상수가 적은 경우는 탄성 효과에 의해 충돌면에서 탄성파가 빠르게 전파 됨을 알 수 있다. 하지만 감쇠 상수가 증가하면 충돌면에서 점성효과가 증대되어 충돌면 부위 이외의 대부분에서 초기 충돌 속도로 봉이 계속 하강함을 알 수 있다.

장시간 전단 계수를 증가시키고 이를 단시간 전단 계수와 동일하게 하여 인위적으로 소성 효과를 제거하기 위해, Figure 5와 Figure 6과 같은 조건, 즉 밀도, 체적 탄성 계수를 각각 1.0(g/cm³), 0.14(GPa), 550(GPa)으로 고정하고 단시간 전단 계수 및 장시간 전단 계수를 모두 140(MPa)로 동일하게 수정 하였다. 이때, 감쇠 상수를 6.5, 65, $650\left(\frac{1}{\mu s}\right)$ 으로 세가지 경 우를 사용하여 MPM으로 해석한 결과를 Figure 7에 나타내었다. FEM의 경우는 x방향 변위로 왼쪽에, MPM의 경우는 수직방향의 충돌 속도로 오른쪽에 각각 나타내었다.

Figure 7. (a) β = 6.5(1/μs) (b) β = 65.0(1/μs) (c) β = 650.0(1/μs) for FEM (left) and MPM (right), respectively.

Download Original Figure

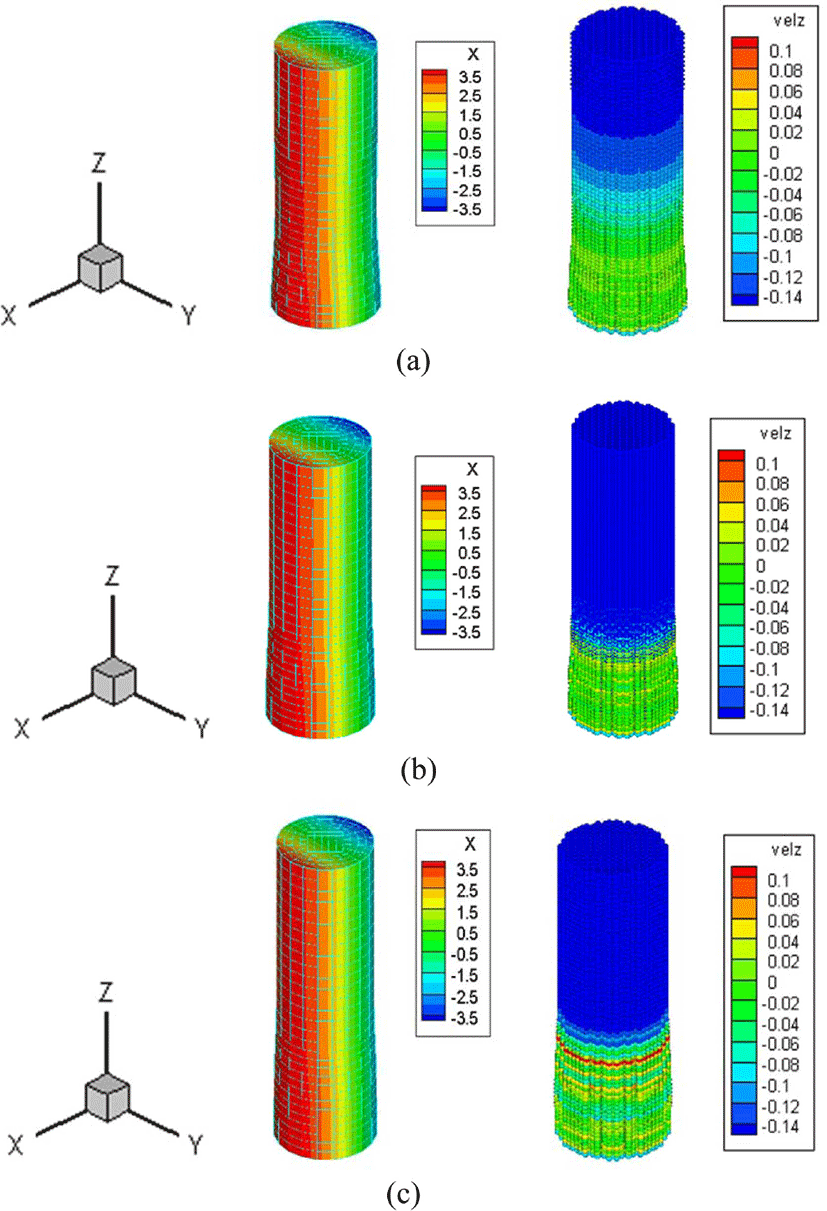
Figure 7에서 알 수 있듯이, 두 FEM과 MPM 두 해석 결과 변형 형상이 동일 함을 알 수 있다. 또한 여기서는 장시간 전단 계수와 단시간 전단 계수와 인위적으로 동일하게 하였기 때문에 소성에 의한 변형은 일어나지 않고 탄성파가 봉 길이 방향으로 전파하는 것을 알 수 있다. 즉 충돌면에서 버섯 모양의 소성 변형이 관찰 되지 않음을 알 수 있다. 이러한 결과로부터 본 연구에서 진행된 선형 점탄성 MPM 모델링은 안정함을 확인 할 수 있다.

Conclusions

고 변형률 속도 조건에서의 고분자 변형은 보호 차폐 및 보호 장치와 같은 내 충격성 응용 분야에서 고려해야 할 주요 요인이다. 테일러 충격 시험은 이에 대한 기초 실험으로 연구가 진행되었으며 재료 특성에 따라 로드의 변형 특성을 찾기 위한 많은 이론적 및 실험적 연구의 주제가 되어 왔다. 본 연구에서는 선형 점탄성 재료에 대하여, FEM 해석을 기반으로 한 입자 기반 충돌, 대 변형으로 인한 파괴 등에 응용하기 위해 MPM 수치 방법을 도입하였고⁹ 이를 바탕으로 본 연구에서는 FEM 수치 해석 기법을 기본으로 하여, 점탄성 재료의 입자 기반 해석 모델 수립 및 프로그램 구현을 완성하였다. 이를 점탄성 봉에 대한 테일러 충격 시험에 도입하여 FEM 결과와 비교하여 본 연구에서 구현한 선형 점탄성 입자 기반 MPM 프로그램 해석 결과를 검증하고 분석하였다. 본 연구에서는 점탄성 변형 거동에 대한 MPM의 구현이 안정적이고 성공적임을 확인하였다. MPM을 사용하면 향후 입자 간 충돌로 인한 요소의 변형 및 파손에 따른 재료 거동을 추가로 고려하여 삼차원 다층 판재 간 파괴가 고려된 충돌 시뮬레이션을 수행할 수 있다. 또한 이 모델링 및 수치 적 접근법은 보다 복잡한 점탄성 재료 시스템, 즉 다층 레이어의 플랙시블 디스플레이의 점탄성 변형 거동 및 피로 파괴, 타이어 충돌 및 피로 파괴 등의 대 변형 및 피로 파괴 거동에 대한 기본 이해 및 적용을 위해 응용될 수 있을 것이다.