Introduction
전 세계적으로 도시철도, 고속철도에서 콘크리트궤도의 부설이 점차 증가하고 있는 추세이다. 콘크리트궤도에서 필수적으로 사용되고 있는 레일체결장치는 철도에서 레일과 침목 또는 하부지지체를 체결하며 궤간 및 레일경사 유지, 하부로 전달되는 충격하중 완화, 레일에 작용하는 윤중 및 횡압 분산, 레일 종방향 변위 억제, 레일과 침목 사이의 전기절연 등 다양한 역할을 담당하고 있다.1 그 중 탄성패드는 레일 직하부에 레일패드와 베이스플레이트를 두고 그 하부에 삽입되어 레일체결장치의 탄성재 역할을 담당하며, 일반적으로 탄성이 우수한 폴리우레탄이나 EPDM 재질이 사용된다. 이러한 탄성패드는 철도현장에서 체결스프링으로 연결되어 초기 압축하중을 받은 상태로 레일의 온도가 −10~70℃까지 변화하는 혹한기, 혹서기의 환경조건에 노출되고, 열차주행 시 열차의 반복하중을 지속적으로 받는 궤도 구성품이기 때문에 탄성패드의 열화로 인한 스프링상수의 변화가 발생하게 된다. 탄성패드의 스프링상수가 증가하게 되면 궤도의 적정탄성을 유지할 수 없게 되어 궤도하부로 전달되는 하중 분산효과 감소, 충격하중 증가 등으로 인한 하부 침목 등 구조물의 손상을 유발할 수 있어 유지보수비의 증가로 이어진다.2 현재 탄성패드의 스프링상수 변화율은 초기에 측정한 정적 스프링상수 대비 반복하중의 크기에 의한 피로시험 후 측정한 정적 스프링상수를 백분율로 계산하여 평가하고 있으며, 재료의 물성은 노화시험 전후 인장강도/신장률(KS M 6518) 변화율과 영구압축률(ISO 1856)로 관리되고 있다. 그러나 재료의 물성이 스프링상수 변화율과 상호 연관성이 떨어지고, 특히 압축 변형에 대한 복원력을 평가하는 영구압축률이 스프링상수 변화율에 대해 상대적인 성능을 비교하거나 가늠할 수 있는 결과와 경향을 보이지 못하는 실정이다. 따라서 탄성패드의 재질과 조성 등을 변경할 때마다 피로시험이 필수적으로 요구되면서 많은 비용과 시간이 소요되고 있으며, 탄성패드의 내구성 향상을 위한 재료 개선 연구에 큰 애로사항으로 작용하고 있다.
본 연구에서는 변경된 영구압축률 시험조건을 적용하여 영구압축률과 스프링상수 변화율의 관계를 확인하고자 하였다. 시험편의 정적 스프링상수 측정은 탄성패드의 정적 스프링상수를 측정하는 하중과 동일한 응력이 가해지도록 시험 하한 하중(F1)과 시험 상한 하중(F2) 및 최대하중(Fmax)에 대해 단면적에 대한 하중 비를 계산하여 적용하였고, 예비하중 인가 방식이 다른 두 가지 방법으로 측정하여 비교하였다. 3개의 온도 조건(70℃, 85℃, 100℃)에서 최대 2000 h 까지 압축노화를 진행하였고, 압축은 탄성패드의 정적 스프링상수를 측정하는 하중 구간에서 최대하중(Fmax)을 가했을 때의 변위로 설정하였다. 측정된 결과는 아레니우스 관계식(Arrhenius equation) 을 이용하여 정적 스프랑상수가 10% 증가한 시점을 기준으로 수명을 예측하였다.
Experimental
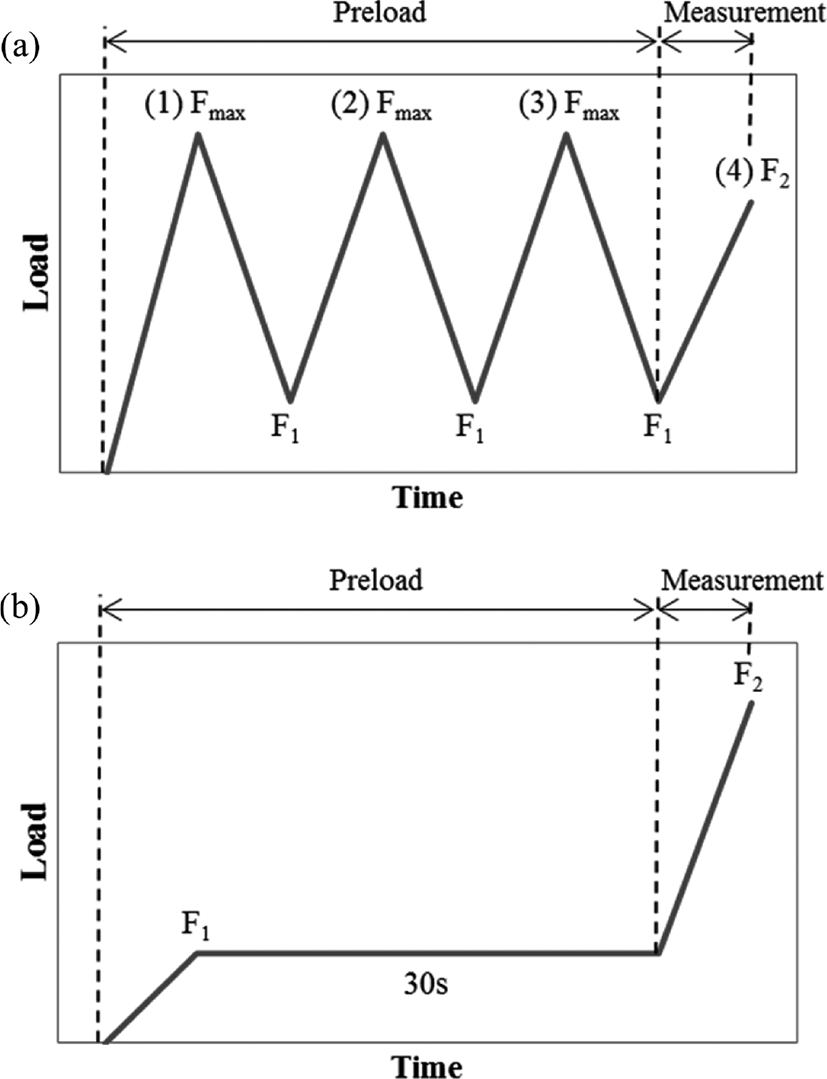
본 실험에서는 제품 두께가 12 mm인 폴리우레탄 발포체로 제작된 탄성패드를 50 mm × 50 mm의 크기로 절단한 시험편이 사용되었다. 사용된 탄성패드의 정적 스프링상수를 측정하는 하중 구간에서의 최대하중(Fmax)이 인가되었을 때의 변위는 3.5 mm이고, 따라서 이를 영구압축률 시험에 반영하고자 압축 시험 장치에 두께가 8.5 mm인 스페이서를 사용하여 3.5 mm의 압축 조건으로 진행하였다. 각각 70℃, 85℃, 100℃에서 노화 시간을 최대 2000 h 까지 일정 시간 간격으로 꺼내어 영구압축률과 시험편의 정적 스프링상수를 측정하였다. 시험편의 정적 스프링상수를 측정하기 위해 만능재료시험기 (SHIMADZU, AG-X plus, 50kN)가 사용되었으며, 시험편의 측정 하중 구간은 탄성패드의 정적 스프링상수 시험 방법 (KRS TR 0014-15R C, D 형식)에서 시험 하한 하중(F1)과 시험 상한 하중(F2) 및 최대하중(Fmax)을 응력으로 환산하여 시험편에 동일한 응력이 인가되도록 Table 1과 같이 설정하였다. 영구압축률 시험을 진행한 시험편은 3.5 mm만큼 압축변형 이력에 대한 영향을 고려하여 Figure 1과 같이 예비하중 인가 방식이 다른 두 가지 방법으로 측정하였다. 시험속도는 1.5 kN/min으로 수행되었으며, Figure 1(a)는 표준 시험방법으로 최대하중(Fmax)까지 3회 인가 후 시험 하한 하중(F1)부터 시험 상한 하중(F2)까지 인가하여 측정하였고, Figure 1(b)는 변형 시험방법으로 시험 하한 하중(F1)에서 30초간 유지 후 시험 상한 하중(F2)까지 인가하여 측정하였다.
| Resilient Pad | Specimen | |
|---|---|---|
| Area (mm2) | 38,537 | 2,500 |
| F1 (kN) | 18 | 1.168 |
| F2 = Fmax × 0.8 (kN) | 68 | 4.411 |
| Fmax (kN) | 85 | 5.514 |
가속수명예측은 시간과 온도의 마스터 곡선(master curve) 및 관계식으로 표현되는 아레니우스(Arrhenius) 모델을 이용하였다. 아레니우스 모델은 여러 온도에서 재료의 초기 특성 값의 일정 변화가 발생하는 시점을 수명으로 판단하여, 시간-온도 관계로부터 특정 온도에서의 예측 수명을 계산할 수 있다. 아레니우스 모델은 식 (1)과 같이 표현된다.
여기서 P는 특성 값, P0는 초기 특성 값, t 는 시간, k 는 반응속도상수(reaction rate constant) 이다. 식 (1)에서 반응속도상수 k는 특성 값 P의 노화반응을 나타내는 정수로 S. Arrhenius에 의해 식 (2) 및 (3)의 실험적 관계가 성립하고 있음이 발표되었다.
식 (2)에서 A는 반응상수, R은 기체상수(gas constant, 8.314 J/mol∙K), T는 절대온도(Absolute temperature, K), E는 활성화 에너지(Activation energy, J/mol) 이다. 식 (3)에서 lnK는 –E/R의 기울기를 갖는 1/T와의 선형적인 관계를 보인다. 식 (1)에서 특성 값 P가 되는 노화 시점을 수명이라고 하면, 그 시점의 수명 t는 식 (4)를 통하여 얻을 수 있다.
식 (4)에서 수명 t는 반응속도상수 관계식인 식 (2)로부터 온도의 관계로 표현되어 수명의 온도 환산이 가능해 진다.3-6
Results and Discussion
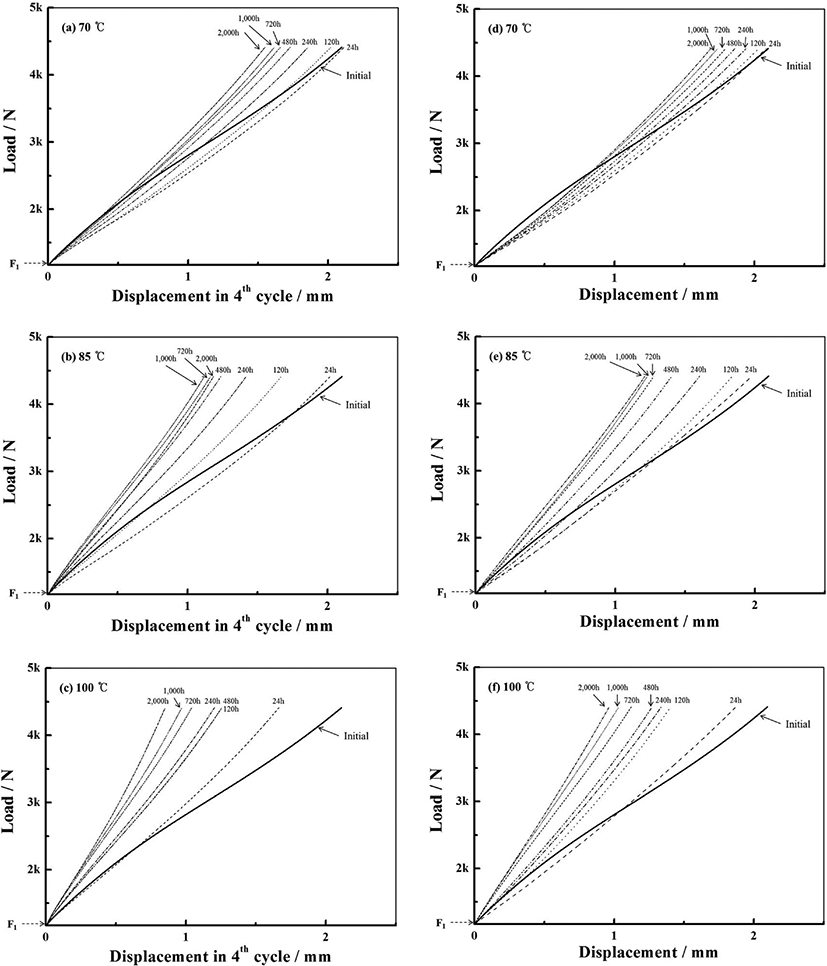
탄성패드에서 절단한 시험편의 초기 정적 스프링상수를 확인하기 위하여 만능재료시험기를 사용하여 Figure 1(a)의 표준 시험방법으로 측정하였다. Figure 2의 결과와 같이 하중을 0 kN부터 Fmax인 5.514 kN까지 인가한 후 다시 F1인 1.168 kN까지 제거하는 첫 번째 압축 사이클에서 탄성 이력현상 (hysteresis)이 크게 나타나고, 두 번째 압축 사이클부터는 재료의 점탄성(viscoelastic)에 의한 Mullins 효과로 설명되는 응력 연화(stress softening) 현상을 보이는데, 하중 F1에 대응하는 변위 d1이 압축 사이클에 따라 소폭 증가하는 경향을 확인할 수 있다.7,8 탄성패드 시험편의 스프링상수는 네 번째 압축 사이클에서 F1과 F2에 대응하는 변위 d1과 d2의 차이에 대하여 kN/mm의 단위로 표현된다.
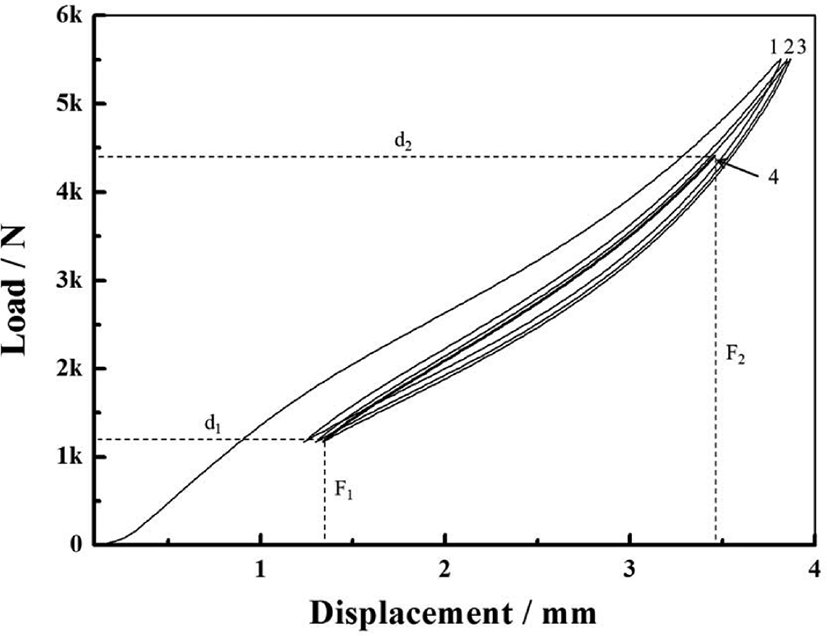
Figure 3에서 압축 노화 시험을 진행한 시험편에 대해 정적 스프링상수를 측정한 하중-변위 곡선을 비교하였다. Figure 3(a)~(c)는 Figure 1(a)의 표준 시험방법으로 측정한 후 네 번째 하중-변위 곡선을, Figure 3(d)~(f)는 Figure 1(b)의 변형 시험방법으로 측정하여 시험 하한 하중 (F1) 에서 30초간 유지 후 다시 하중을 인가하는 시점부터 하중-변위 곡선을 나타내었다. 측정된 스프링상수는 Table 2에 나타내었고, 모든 결과에 대하여 압축 노화 시간이 증가할수록 하중-변위 곡선의 기울기인 스프링상수가 증가하는 것을 확인할 수 있다. 압축 노화 온도가 높을수록 스프링상수의 변화가 크고, 각각의 온도에서 노화 초기에 스프링상수가 큰 폭으로 증가한 이후에 다시 변화 폭이 감소하는 경향을 나타낸다. 초기 상태의 하중-변위 곡선과 비교하여 압축 노화를 진행한 시험편은 보다 선형에 가까운 거동을 보였다. 따라서 초기 상태의 하중-변위 곡선을 기준으로 1차 변곡점 이전의 구간에서 압축 노화 후 시험편의 하중-변위 곡선의 기울기가 더 낮음에도 불구하고 전체 측정 하중 범위에 대한 스프링상수는 더 높게 측정되는 현상을 확인할 수 있다. 또한 노화 후 동일한 시험편에 대해서 Figure 3(a)~(c)의 기울기가 (d)~(f)보다 더 높게 나타나는데, 이는 예비하중으로 최대하중(Fmax)을 3회 인가하면서 압축변형 이력이 영향을 미치는 것으로 판단된다. 압축변형 유지와 고온에 의한 물리적∙화학적 열화(degradation)로 예비하중에 응답(response)하지 못하는 비탄성(inelastic) 영역의 영향이 반영될 수 있고, 더불어 응력 연화(stress softening) 현상으로 나타나는 Mullins 효과를 증가시켜 네 번째 사이클에서의 시험 하한 하중(F1)에 대응하는 변위(d1)의 증가를 일으키는 것으로 사료된다. 결과적으로 시험편의 변형이 더 큰 상태에서 스프링상수가 측정되므로, 하중이 증가할수록 하중-변위 곡선의 기울기가 상대적으로 크게 증가하는 경향을 확인할 수 있다. 이러한 현상은 본 연구에서 수행한 압축 노화 시험에 대한 스프링상수의 변화를 파악하는데 영향을 미치며, Figure 3(b)의 2,000 h 및 Figure 3(c)의 480 h 시험편의 스프링상수가 경향성을 벗어나는 결과를 야기한 것으로 판단된다. 따라서 압축 노화 시험을 통해 영구변형이 스프링상수의 증가에 미치는 영향을 확인하기 위한 실험에는 표준 시험방법보다 변형 시험방법을 사용하는 것이 더 적절하다는 결론을 얻을 수 있었다.
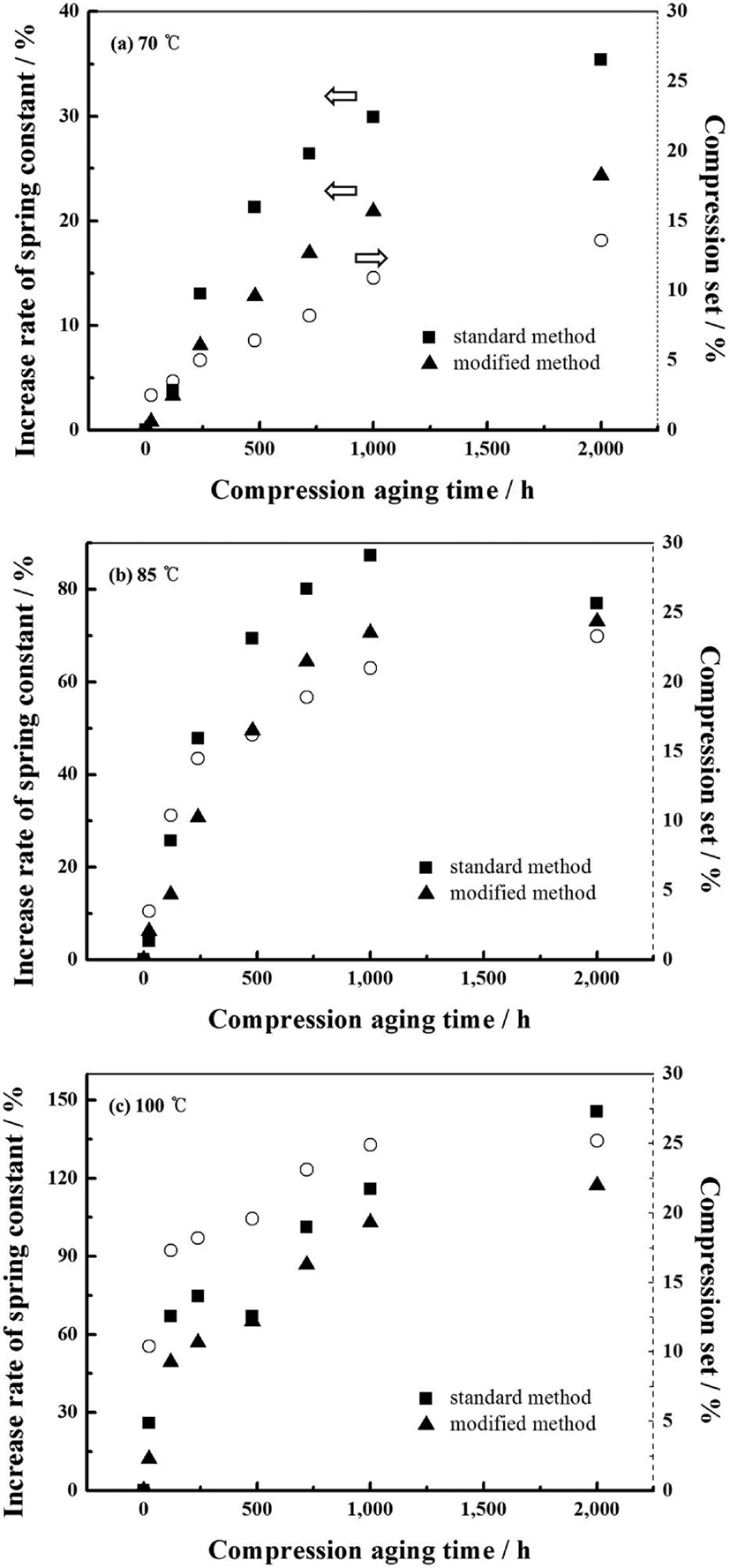
압축 노화를 진행한 시험편에 대해 표준 시험방법과 변형 시험방법으로 측정한 스프링상수를 영구압축률과 비교하여 Figure 4에 나타내었다. 두 시험방법으로 측정한 스프링상수는 모두 영구압축률의 증가와 유사한 경향을 보이지만, 앞서 언급한 이유로 표준 시험방법으로 측정한 스프링상수가 변형 시험방법으로 측정한 결과보다 높은 증가 폭을 나타낸다. 압축 노화 초기에는 영구변형이 발생하더라도 스프링상수의 변화가 상대적으로 적은 폭으로 증가하지만, 노화가 진행되면서 영구변형이 적게 발생하더라도 스프링상수는 크게 증가한다. 이는 스프링상수 증가에 영구변형 뿐만 아니라 우레탄 소재의 화학적 열화로 인한 경화(hardening)가 동반된 것으로 사료된다. 또한 본 실험 결과에 대해 스프링상수를 증가시키는 요인을 화학적 열화와 영구변형만을 고려하면, 화학적 열화가 상대적으로 서서히 진행되고 영구변형이 일정수준에서 수렴하는 경향을 나타내더라도 화학적 열화는 지속적으로 발생한다고 판단할 수 있다.
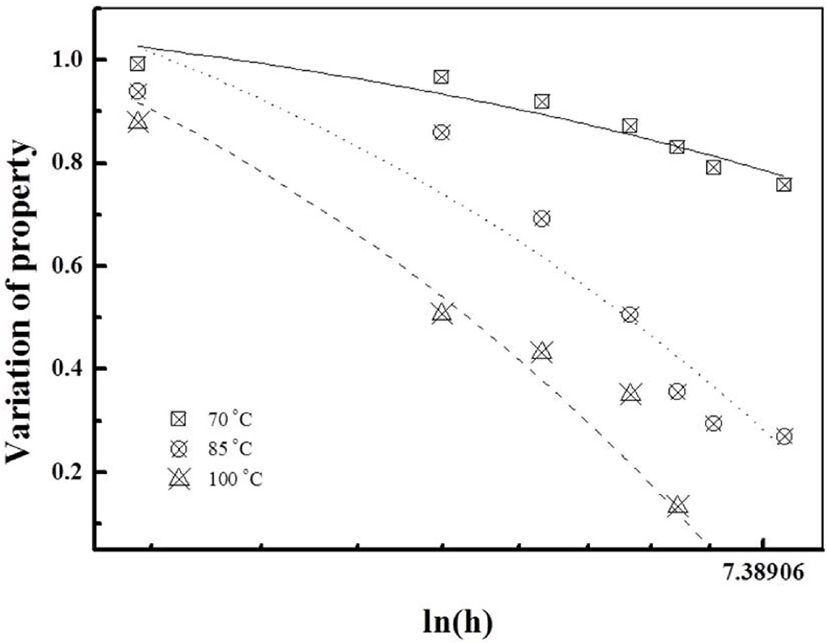
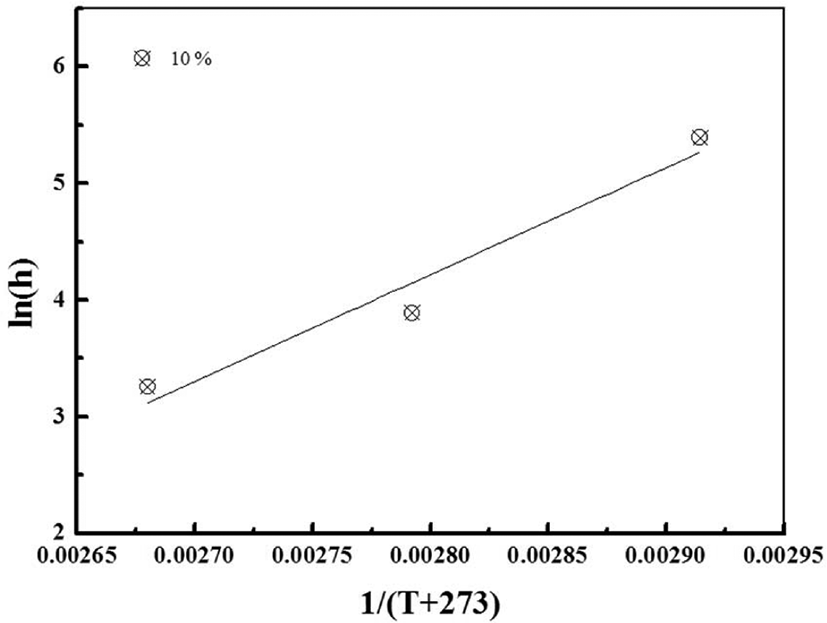
탄성패드 시험편의 가속수명예측을 위해 Figure 5와 같이 시간의 자연로그 값으로 하여 초기 특성 값을 기준으로 변화율을 나타내었다. 식 (4)를 이용하여 탄성패드의 스프링상수 변화율로 구해진 반응속도상수(K)와 기체상수(R), 절대온도(T)를 통해 구해진 활성화에너지(E)는 98,266 J/mol이다. 현재 레일체결장치의 탄성패드는 피로시험 전후 스프링상수 변화율로 관리되고 있으며, 세계최고수준의 탄성패드 제품은 10% 이내의 성능을 나타내고 있다. 따라서 이를 반영하여 Table 3에 나타낸 것과 같이 탄성패드 시험편의 사용수명을 스프링상수 변화율이 10%일 때라고 가정하면 ln(h)은 70℃, 85℃, 100℃에서 5.39, 3.89, 3.26이 된다. 이러한 온도와 시간의 관계로부터 Figure 6과 같은 아레니우스 선도를 구한 다음, 최소제곱법을 이용하여 계산한 수명예측식을 Table 4에 나타내었다. 탄성패드에 지속적으로 최대하중이 가해지는 조건에서 노출되는 사용온도가 30℃, 40℃, 50℃이면, 스프링상수 변화율이 10% 이하로 유지될 수 있는 기간은 도출된 수명예측식을 활용하여 약 273일, 104일, 42일이라고 예측할 수 있다.
| Variation of property | ln(h) | ||
|---|---|---|---|
| 70°C | 85°C | 100°C | |
| 10% | 5.39 | 3.89 | 3.26 |
| Variation of property | Arrhenius equation | Lifetime (h) | ||
|---|---|---|---|---|
| 30°C | 40°C | 50°C | ||
| 10 % | ln(t) = −21.42+9,158/(T+273) | 6,553 | 2,497 | 1,010 |
Conclusions
본 연구에서는 탄성패드의 영구압축률이 스프링상수 변화율에 미치는 영향을 확인하고자 변경된 압축 노화 시험과 스프링상수 측정방법을 제안하였다. 압축 노화 시험을 통해 영구변형이 발생한 시험편에 대하여 스프링상수를 측정할 때 압축변형 이력에 의한 영향으로 인해 예비하중을 시험 하한 하중(F1) 이상으로 인가하는 것이 적절하지 않다는 결론을 얻을 수 있었다. 실험을 통해 영구압축률과 스프링상수 변화율이 매우 유사한 거동을 보이면서도 화학적 열화가 지속적으로 발생하는 것을 확인할 수 있었다. 측정된 결과를 통해 아레니우스 관계식을 이용하여 수명예측식을 도출하였고, 탄성패드에 지속적으로 최대하중이 가해지는 조건에서 노출되는 사용온도가 30℃일 때 스프링상수 변화율이 10% 발생하기까지 약 273일이 소요됨을 예측할 수 있었다. 본 연구를 통해 탄성패드의 스프링상수 변화율에 대한 영구압축률의 영향을 확인하였고, 이는 탄성패드의 내구성을 확인하는 간소화된 시험편 평가방법을 도출하는데 기초 결과로 활용될 수 있을 것이다.