Structure Analyses of Rubber/Filler System under Shear Flow by Using Time Resolved USAXS Method

The rubber and the fillers used in this study are Liquid polyisoprene (PI) from Kuraray Co. Ltd. (LIR-50, number-averaged molecular weight M_w = 54,000) and carbon black (CB) (N326, Specific surface areas measured using nitrogen adsorption method 81 m²/g, Dibuthyl phthalate adsorption for the CB filler 75 cm³/100 g, arithmetic average particle diameter 28 nm), respectively. The volume fraction of CB is 10%. The PI and CB were dissolved into a solution with toluene in which total weight fraction of the rubber/filler are 10%. The mixture was obtained by evaporating the solvent.

We measured the scattering intensity under shear flow by using time-resolved USAXS. Time-resolved USAXS measurement was carried out at BL19B2 and BL20XU in SPring-8, Japan. At BL19B2, the X-ray energy and the sample-to-detector distance were respectively 24 keV and 40 m and the scattering vector q range is, thus, from 0.008 nm⁻¹ to 0.2 nm⁻¹, where q is the magnitude of the scattering vector defined by q = (4π/λ)sin(θ/2) with λ and θ being the wavelength of the incident beam and the scattering angle in the medium, respectively. At BL20XU, the X-ray energy and the sample-to-detector distance were respectively 23 keV and 160 m. With this USAXS configuration of BL20XU, the q range of 0.003 to 0.02 nm⁻¹ is partially overlapped with those of USAXS results of BL19B2, therefore we can widen observable q-range by combining the USAXS measurement of BL19B2 with that of BL20XU. All measured intensities were averaged in the direction of parallel and perpendicular to the shear flow after corrections for the sample transmittance, and the scattering from the empty cell used in this experiment.

To impose shear flow, we used a heating shear stage for SAXS, CSS450WX (LINKAM SCIENTIFIC INSTRUMENTS). Measurement temperature is 140ºC and shear rate is 10 s^-1. The X-ray was introduced along the direction perpendicular to the plates or the velocity gradient direction Oy. The detecting plane was set to the Oxz plane, where Ox axis is the shearing direction and Oz axis is the vorticity or neutral direction.

Figure 1 shows the scattering intensity obtained from the BL19B2 and BL20XU data in the direction of parallel and perpendicular to the shear flow after the onset of shearing. Solid lines are the scattering intensity parallel to the shear flow and broken lines are the scattering intensity perpendicular to the shear flow. From the figure, we can see two power-law behaviors and the one shoulder immediately after the start of shearing (0 sec), indicating that the carbon black has already formed the hierarchical structure immediately, as suggested by the earlier works. At the high q region (0.13 <q <0.2 nm⁻¹), the slope is 3.5, suggesting that surface fractal dimension D_s of the primary particles is 2.5. Around q = 0.07 nm⁻¹, the shoulder appears. This shoulder is originated from the aggregate of primary particles. At the low q region (0.004 < q <0.01 nm⁻¹), the slope is 2.9, suggesting that aggregates make network structure with mass fractal dimension D_m = 2.9.

Figure 1. The scattering profile combined BL20XU and BL19B2 data is plotted as a function of q at 0 sec, 1800 sec and 5280 sec after the start of shearing.

Download Original Figure

The scattering intensity perpendicular to the shear flow is larger than that parallel to the shear flow in the q range from 0.004 to 0.01 nm⁻¹. At 0 sec, the size of agglomerate, which is upper limit of the mass fractal structure consisting of the aggregates is macroscopic scale and beyond over this q-range. The anisotropy of the scattering pattern indicates that the agglomerate elongates by shear flow.

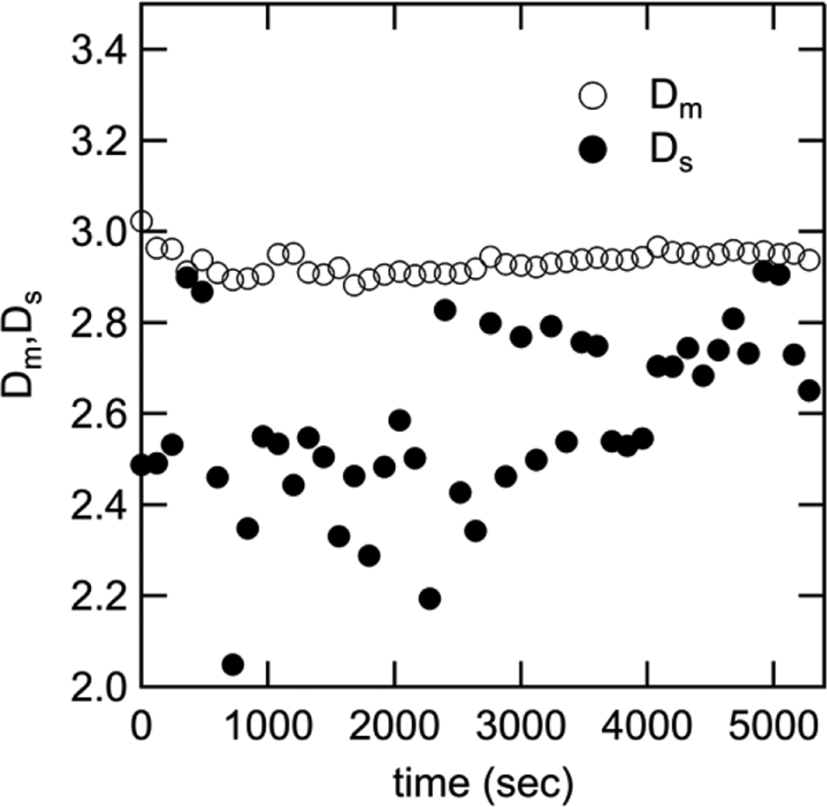
At 1800 sec and 5280 sec after the shear applied, the scattering intensity increases with time, indicating that the number of agglomerate and aggregate increases with time. We can still observe the power-law behavior of 2.9 at q < 0.01 nm^-1 but the deviation from the power-law becomes more significant around q = 0.005 nm⁻¹ with time. This tendency suggests that the mass fractal dimension of aggregate doesn’t change and the size of agglomerate R_g is detected in this q-range at 1800 sec and 5280 sec because the agglomerate was broken and becomes smaller by shear flow. In addition, the scattering patterns is anisotropic around 0.005 nm⁻¹ at 1800 sec and 5280 sec, indicating the agglomerate elongates by shear flow. On the other hand, the shoulder around 0.07 nm⁻¹ doesn’t change with time and is isotropic, suggesting that the size and shape of aggregate is not affected by shear flow. The surface fractal of the primary particle also maintains 2.5.

In order to analyze the hierarchical structure quantitatively, we applied Unified Guinier/Power-law approach to the scattering profiles.^16-18

This equation can explain the hierarchical structure of the filler in the rubber/filler systems quantitatively and the scattering intensity I(q) is expressed by

where R_g, R, D_m, D_s are, respectively, the radius of gyration of the agglomerate, the radius of gyration of the aggregate, the mass-fractal dimension of the aggregate, and the surface fractal dimension of the primary particles. G, A, B, C are expressed by

and P=6−D_s, where ρ, N_A, V_A, N_B, V_B are, respectively, the electron density difference between the CB and the PI, the number of agglomerate, the volume of an agglomerate, the number of aggregate, the volume of a silica particle. The value of parameters G, R_g, A, D_m, R, B, C, D_s can be obtained by applying this equation to the scattering profiles.

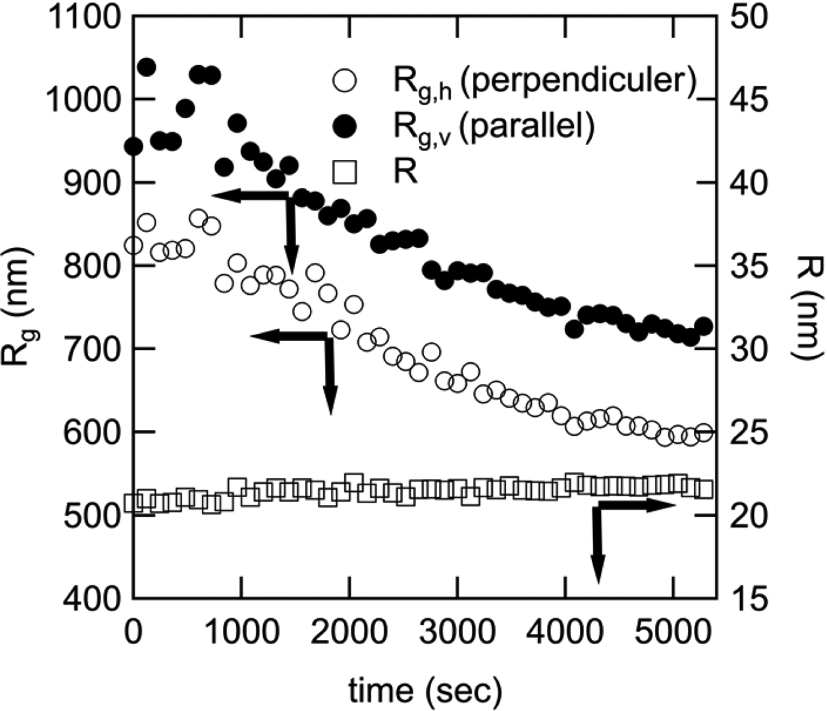
Figure 2 shows the change of the size of agglomerate in the direction of parallel to the shear flow (R_g,v) and perpendicular to the shear flow (R_g,h), and the size of aggregate with time. At 0 sec, R_g,v is larger than R_g,h, suggesting that agglomerate elongation by shear flow in the direction of shear flow as mentioned above. As time increases, R_g,h and R_g,v decrease monotonically, indicating the elongated agglomerate is peeled from surface. On the other hand, R doesn’t change very much. The aggregate isn’t affected by shear flow.

Figure 2. The size of agglomerate in the direction of perpendicular and parallel to the shear flow and the size of aggregate with time.

Download Original Figure

As the number of aggregate of an agglomerate is N₀, N_A and V_A are given by

Then G/B is expressed by

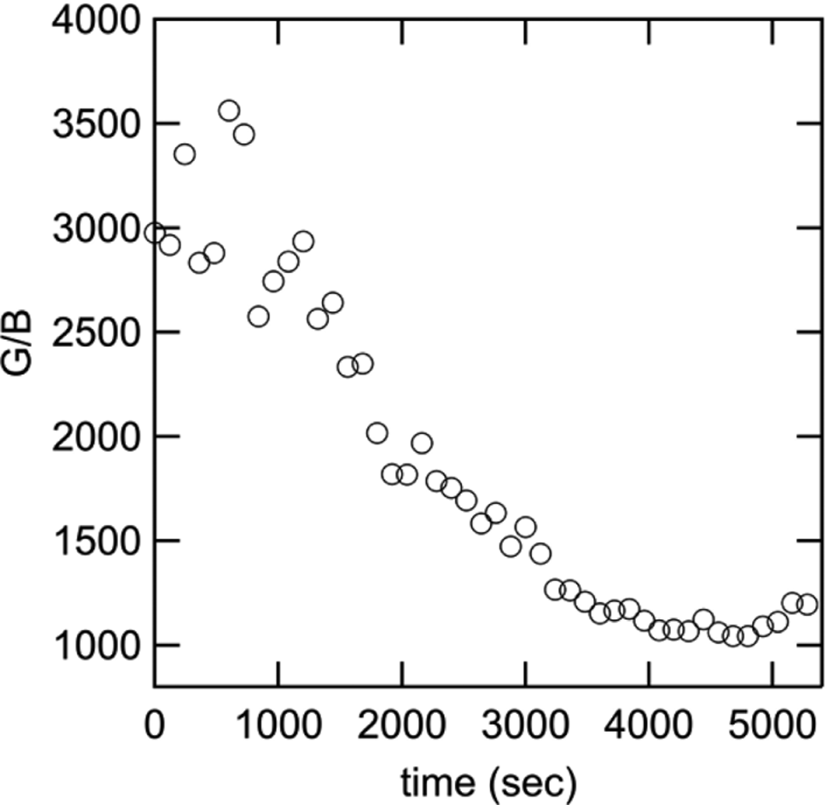
Therefore, G/B means the number of aggregate an agglomerate. Figure 3 shows G/B as a function of time. At 0 sec, G/B equals 3000, suggesting that the aggregate exists 3000 an agglomerate. Under shear flow, G/B decreases as time increases. This is because agglomerate is broken by shear flow. The density of aggregate in an agglomerate doesn’t change because mass fractal dimension keeps 2.9 as shown in Figure 4, indicating that agglomerate doesn’t shrink but is peeled by shear flow. As shown in Figure 4, D_s almost maintains 2.6, suggesting that surface fractal doesn’t change by shear flow.

Figure 3. G/B is plotted as a function of time

Download Original Figure

Figure 4. D_m, D_s is plotted as a function of time.

Download Original Figure

Figure 5. G/R_g⁶ and B/R⁶ is plotted as a function of time.

Download Original Figure

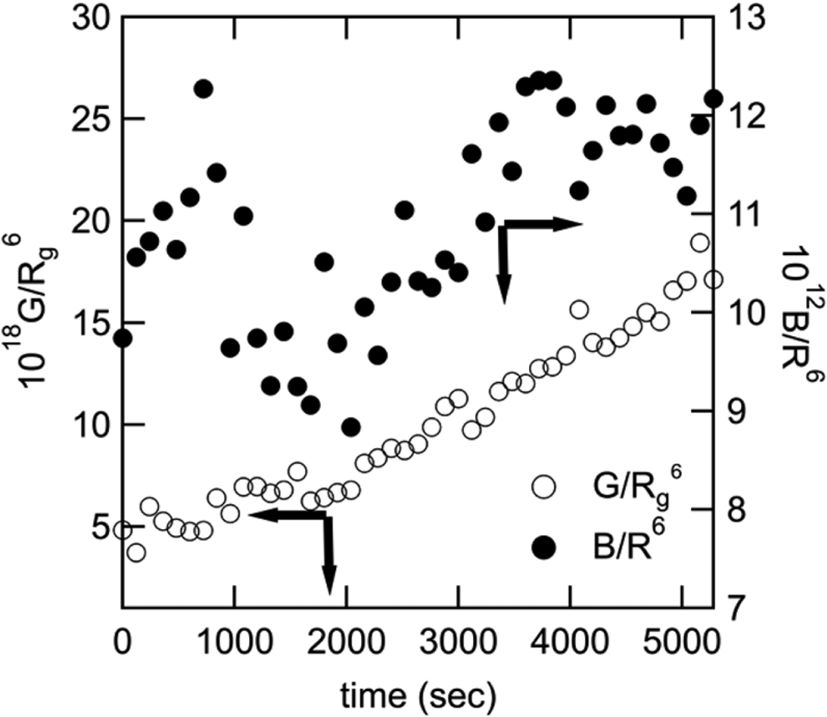
G/R_g⁶ is proportional to N_A and B/R⁶ is proportional to N_B because $V_A\propto R_g^6$ and V_B∝R⁶. Both G/R_g⁶ and B/R⁶ increase monotonically as time increase. This is because the number of agglomerate increase by the destruction of large agglomerate which can’t be detected in q region of this experiment and the aggregate increase by the destruction of agglomerate simultaneously. The aggregate may agglomerate again, but the increasing by distraction is dominant, so B/R⁶ increase as time increase.