Introduction
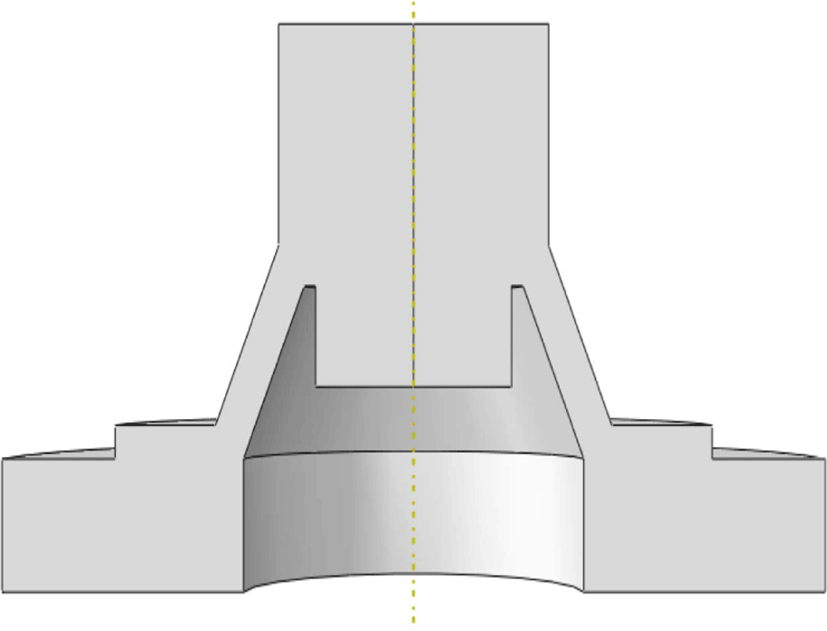
자동차의 파워윈도우 스위치는 윈도우 글라스를 올리고 내리는 작동에 사용된다. 윈도우 스위치는 Figure 1에서 보는 바와 같이 사용자의 손끝에 직접 접촉하는 플라스틱 버튼, 반복 사용 시 원활한 조작 성능을 유지하기 위한 고무패드 부품, 그리고 접점이 닿는 PCB 기판으로 이루어져 있다. 플라스틱 버튼을 누르면 PCB 기판과 고무패드에 붙은 금속 단자가 접촉하게 되어 스위치가 작동하게 된다. 스위치 고무패드는 탄성과 내열성 그리고 내구성이 우수한 실리콘 고무 재질이 주로 사용된다.1
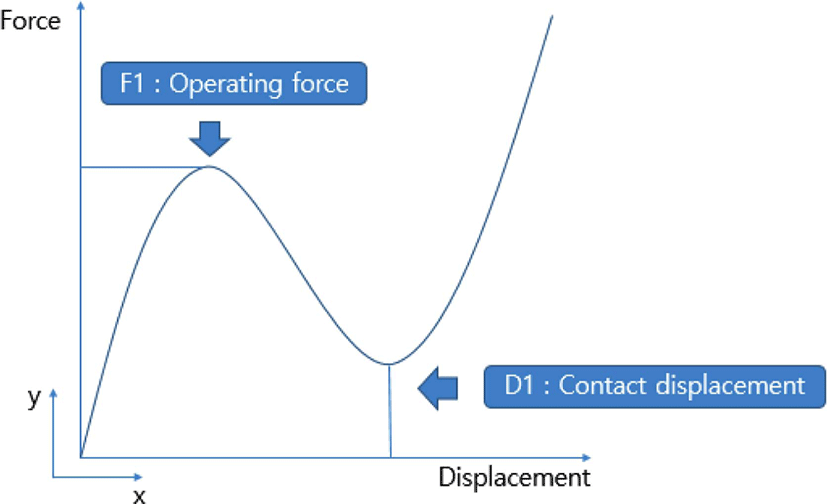
스위치의 성능은 고무패드의 성능에 좌우된다. Figure 2는 전형적인 스위치 고무패드의 하중-변위 선도를 보여준다. 변위가 증대됨에 따라 반발력이 커지다가 다시 감소하게 되며, 이때 극대값을 나타내는 F1 값을 조작력(operating force)이라 부른다. 조작력은 스위치의 정상적인 작동을 위한 중요한 설계 변수로서, 스위치의 작동 성능을 판단하는데 중요한 역할을 한다.
스위치 고무패드 부품은 반복적인 사용에 따른 피로 손상에 의한 고장과 고무 노화에 따른 조작력 변화로 인한 고장이 발생될 수 있다. 피로 손상에 의한 고장 즉 피로수명은 실험실 내에서 고무패드 부품의 피로수명시험을 통해 평가하고 예측할 수 있으며, 고무부품에 대한 피로수명 예측에 대한 여러 선행 연구 결과가 발표되어 왔다.2 본 논문에서는 상대적으로 긴 시간과 많은 노력이 필요하게 되는 노화로 인한 고무패드의 조작력 변화에 따른 수명 예측 방법을 시도하고자 한다.
맨 먼저, 스위치 고무패드 부품과 동일한 고무 재질의 시편을 이용하여 다양한 가속 열 노화시험 조건에서 단축 인장시험을 통해 비선형 재료상수를 구하였다. 각 노화시험 조건에 따른 비선형 재료상수를 이용하여 고무패드 부품의 하중-변위 선도를 유한요소해석으로부터 구하였다. 이로부터 각 노화조건에서의 조작력을 얻었으며, 아레니우스 관계식을 이용하여 여러 조건에서의 노화수명을 산출하였다.
한편, 노화조건에 따른 비선형 재료상수의 변화 경향을 하나의 변수로 나타낼 수 있는 전단탄성계수를 이용하여 아레니우스 선도를 구하였으며, 조작력 변화에 따른 아레니우스 선도로부터 구한 노화수명과 비교 분석하였다.
Nonlinear Material Constants
고무 재료는 일반 탄성체와는 달리 하중과 변형이 비선형 관계를 보이는 대변형 범위에서도 탄성 거동을 나타내는 초탄성 특성을 지닌다. 이러한 고무 재료의 특성은 변형률에너지 함수의 비선형 재료상수로 표현할 수 있다.3
변형률에너지 함수(W)는 연신률 불변량의 함수와 주 연신률의 함수로 (1), (2) 식과 같이 나타낼 수 있다.
여기서, λ1, λ2, λ3는 주 연신률이며, 재료가 등방성인 경우 I1, I2, I3는 다음 (3), (4), (5) 식과 같다.
대부분의 고무 재료는 비압축성이므로 체적 계수는 전단계수보다 상당히 크며 재료가 많이 구속되어 있지 않는 경우에는 비압축성의 가정이 타당함이 알려져 있다. 재료를 비압축성으로 가정하면 λ1, λ2, λ3 = 1이므로, I3 = 1이 되며, 의 관계식이 유도되어 위의 식은 (6) 식과 같이나타낼 수 있다.
비압축성 고무의 변형 해석에 널리 쓰이는 변형률 에너지함수는 연신률 불변량의 함수로 표시되는 다음과 같은 Mooney-Rivlin 함수의 다항식이 흔히 사용된다.
여기서 Cij는 Mooney-Rivlin의 재료상수를 의미하며, 재료시험 결과로부터 결정되는 상수 값이다. N=2 일 때 식 (8)과 같은 2변수 식이 많이 사용된다.
한편, 고무 재료의 전단탄성계수(G)는 탄성 이론에 따르면 다음 식과 같이 정의된다.
유한요소해석을 통하여 고무 부품의 특성을 예측하기 위해서는 우선 고무재료의 비선형 재료상수 값을 알아야 한다. 정확한 비선형 재료상수 값은 여러 가지 시험 모드, 즉 인장, 이축 인장, 전단 시험 모드의 응력-변형률 선도로부터 커브피팅을 통해 구해진다.4 그러나, 여러 종류의 시험을 수행하는 데는 시간과 경비가 많이 소요되는 어려움이 있다. 본 논문에서는 노화에 따른 비선형 재료상수 값의 변화 추세를 알아보는데 주안점을 두어, 시간과 비용을 절감하기 위하여 단순 인장시험만을 수행하여 비선형 재료상수 값을 구하였다.
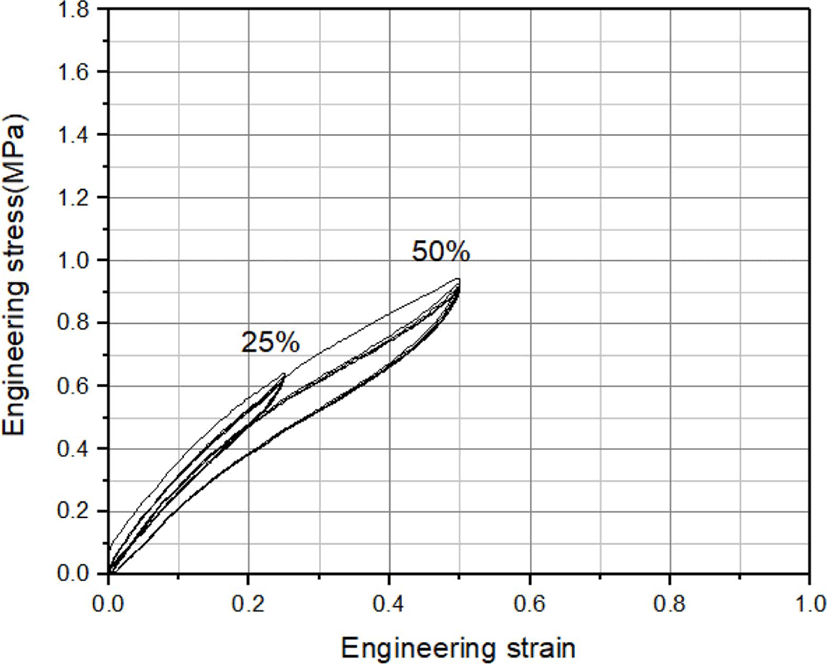
인장시험에 사용된 시편은 스위치 고무부품과 동일한 실리콘 재질의 시트지를 활용하여 컷팅한 KS규격 아령형 3호를 사용하였고, 100 mm/min의 속도로 25%, 50%의 변형률 구간에서 각각 5회의 반복 하중을 가하여 응력-변형률 관계를 획득하였다. 변형률 구간이 클수록 기울기가 감소함을 알 수 있다.
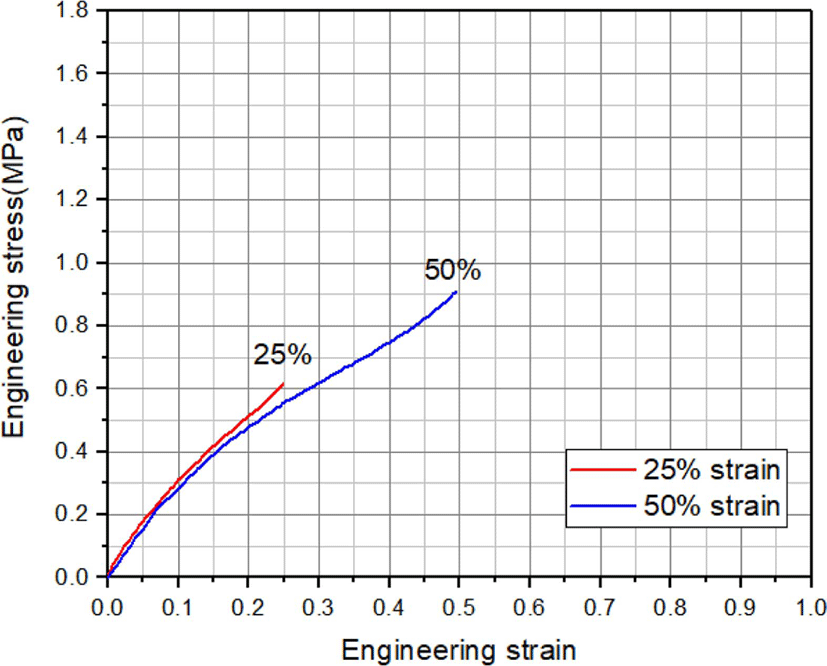
Figure 3은 인장시험으로부터 얻은 대표적인 응력-변형률 히스테리시스 선도를 보여주며, Figure 4는 커브 피팅을 위해 5번째 응력-변형률 선도만을 나타낸 그림이다.
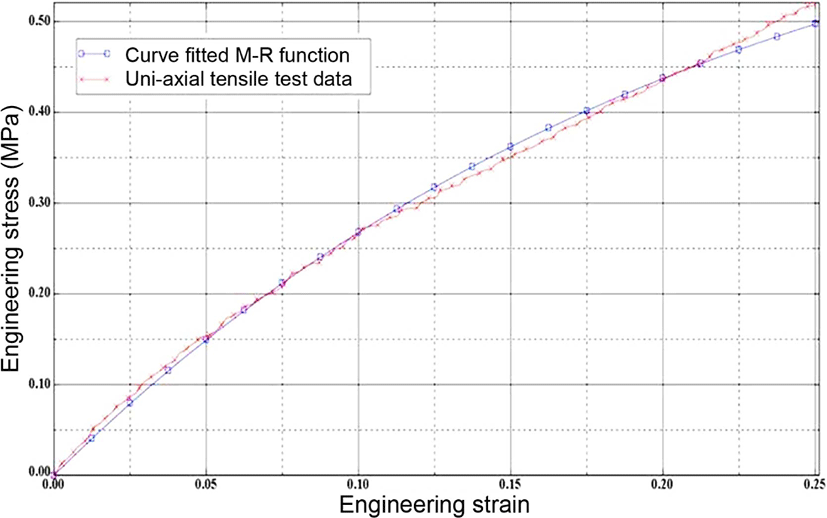
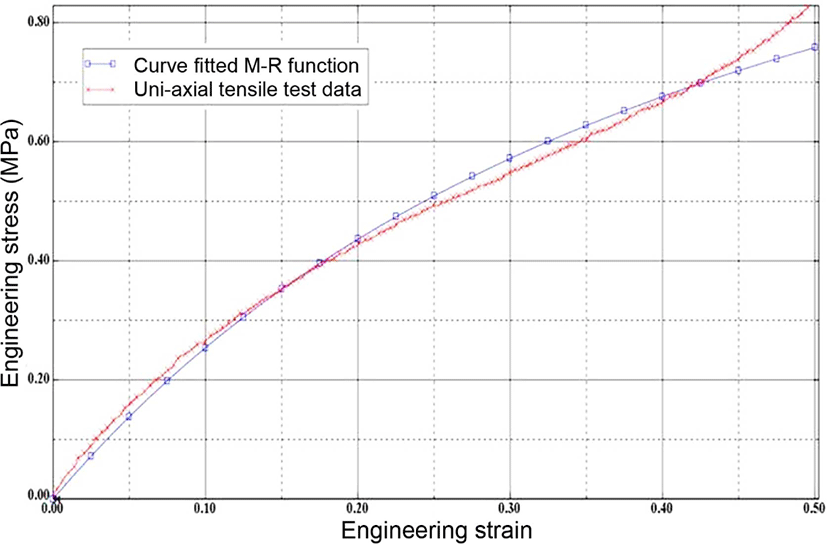
Figure 5와 Figure 6은 25%, 50% 변형률 물성 값에 대한 무니-리블린 함수로 커브 피팅한 선도를 보여준다. 두 개의 그림에서 시험 데이터 선도는 전형적인 비선형성을 보이고 있으며, 커브피팅한 선도는 모노토닉(monotonic)한 응력-변형률 관계를 나타내고 있다. 각각의 변형률 범위 내에서 전체적으로 시험 값과 피팅 값이 잘 일치하고 있음을 알 수 있다.
Aging Test
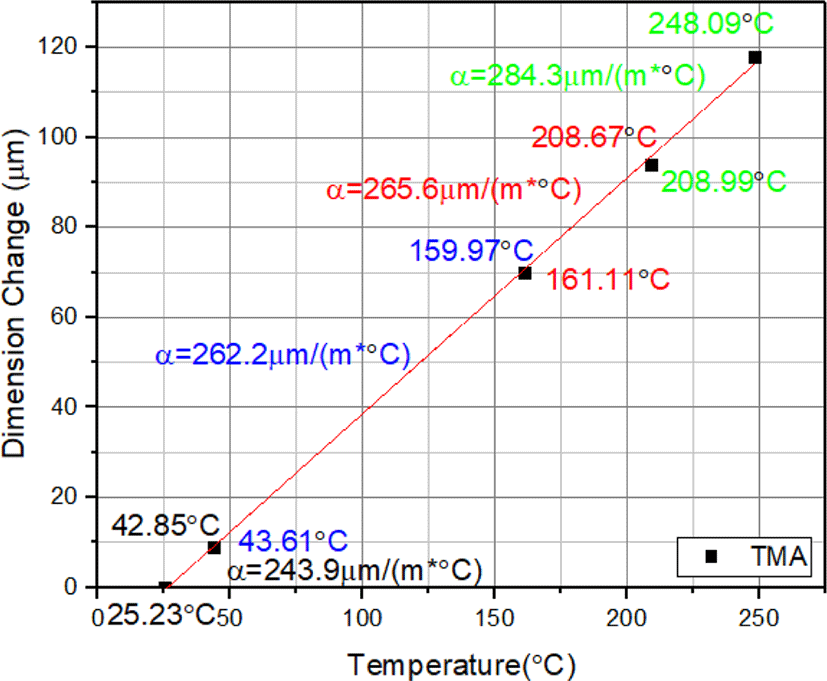
스위치 고무 패드 부품에 대한 장기간의 노화 시간을 단축하기 위해서 고무에 영향을 크게 미치는 열적 요소를 활용하여 가속 열 노화 시험을 수행하여야 한다.5 가속 열 노화 시험은 상온보다 가혹한 조건에서 특정 요인에 대해 빠른 시간 동안 특성을 저하시키는 방법이다. 가속 열 노화 시험을 위해서는 먼저 노화 시험 온도가 결정되어야 한다. 단 시간 내에 가속 계수를 키우기 위해서는 해당 고무 재질에 대한 구조적으로 안정된 가열 온도 범위 내에서 노화 온도를 높여야 한다. 이를 위하여 열 분석 장비를 이용하여 단축인장시험을 실시했던 고무 시편과 동일한 재질의 시편에 대한 열팽창계수를 측정하여 해당 고무 재질에 대한 구조적으로 안정화할 수 있는 가열 온도 범위에 대해서 파악하였다. Figure 7은 스위치 고무 부품과 동일한 재질을 가진 시편에 대해서 열기계 분석시험(TMA) 한 결과이다. 결과를 보면 해당 시편은 248°C까지의 온도 범위 내에서 안정화된 구조를 유지한다는 것을 확인할 수 있었다. 일반적인 실리콘 고무의 경우 250°C 이상의 고온에서의 활용성은 거의 없다고 판단하여 상온 25°C에서부터 고온 250°C까지 시편을 열 분석 시험하여 구조적으로 안정화 되고, 노화 한계점으로 문제가 없는지 여부를 검증하였다.
이를 활용하여 노화 온도에 대한 범위를 248°C 내에서 설정하여 총 150°C, 180°C, 210°C, 240°C 등 4개의 구간으로 분류하여 시편에 대한 구조적 안정성을 보장한 상태에서 노화 시험을 실시하였다.
가속 열 노화 시험은 공기 가열식 챔버를 활용하여 4가지의 온도 조건 (150°C, 180°C, 210°C, 240°C)에서 1일, 3일, 7일, 15일, 30일, 45일, 60일 동안 실시하였다. 노화 시킨 후 고무 시편의 응력-변형률 관계 선도를 통해 얻은 무니-리블린 비선형 재료 상수 값을 구하였다.
Table 1은 50% 변형률 물성 데이터를 활용하여 노화 온도 및 노화 일수에 따른 무니-리블린 상수(M.R.)의 산출 값과 각 경우에서의 전단탄성계수(G)의 산출 값을 보여준다. 240°C 고온의 경우에는 노화 시작 후 7일 이내에서 물성 값이 급격하게 변화하여 7일까지의 노화 시험 데이터를 활용하였다. 고무에 대한 전단탄성계수 값은 G 값으로 나타낸다.6
Prediction of the Operating Force
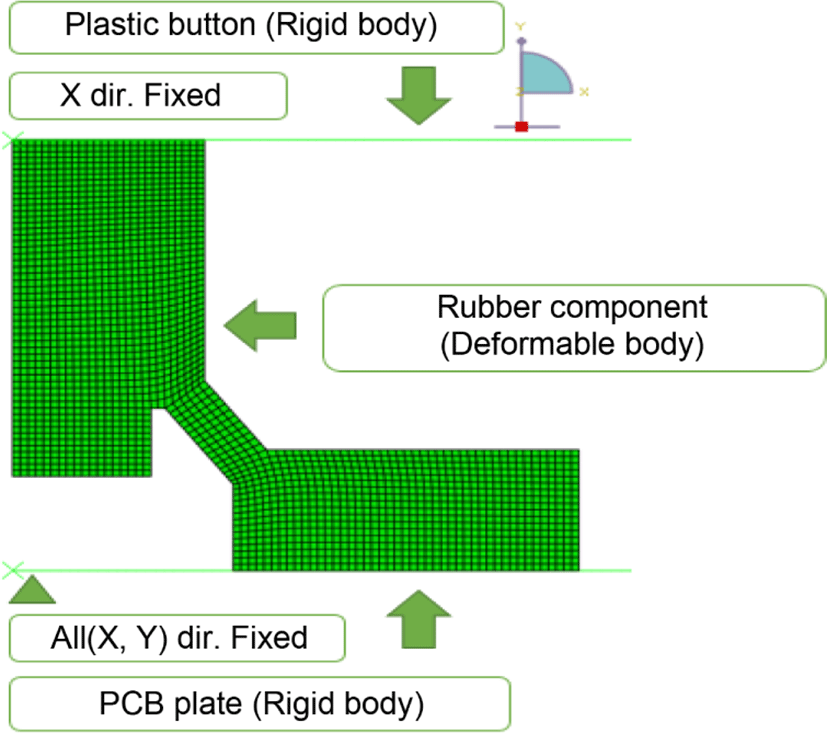
스위치 고무 패드 부품의 조작력 값을 산출하기 위해 유한요소해석을 수행하였다. 유한요소해석을 수행하기 위한 고무 패드 부품의 모형은 Figure 8과 같이 부품의 단면만을 변위 작동 방향인 Y축 대칭으로 모델링하여 수직 변형에 따른 해석을 수행하였다. 구속 조건으로는 수직 변형을 알아보기 위하여 축 대칭(Axi-symmetric) 조건을 사용하였으며, 스위치에 접촉하는 상단과 하단 부위를 강체(Rigid body)로 설정하였다. 하중 조건은 아래 방향으로 단자 접촉까지의 최대 변위 조건을 주어서 해석을 수행하였다. Figure 9는 단일 부품 형상의 절반을 모델링하여 수평 변형에 따른 유한요소 해석을 수행하기 위해 사각형 요소 구조로 구성한 결과이다.
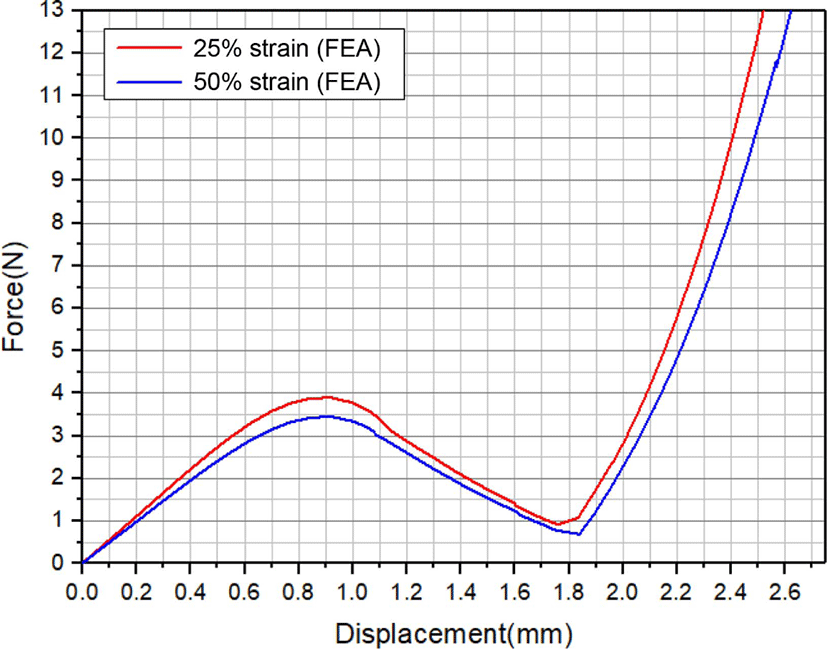
Figure 10은 유한요소 해석에서 얻은 하중-변위 선도이다. 비선형 재료 물성 시험을 통해 얻은 최대 변형률 50%에서의 물성 값 보다 25%에서의 물성 값으로 산출한 하중-변위 선도에서 조작력 값이 더 크게 나타났다. 조작력 발생 위치와 접촉이 발생되는 시점의 위치는 동일하게 나타났으며, 재료 상수 값의 변화에 따른 조작력 값의 상대 비교는 가능할 것으로 판단되었다.
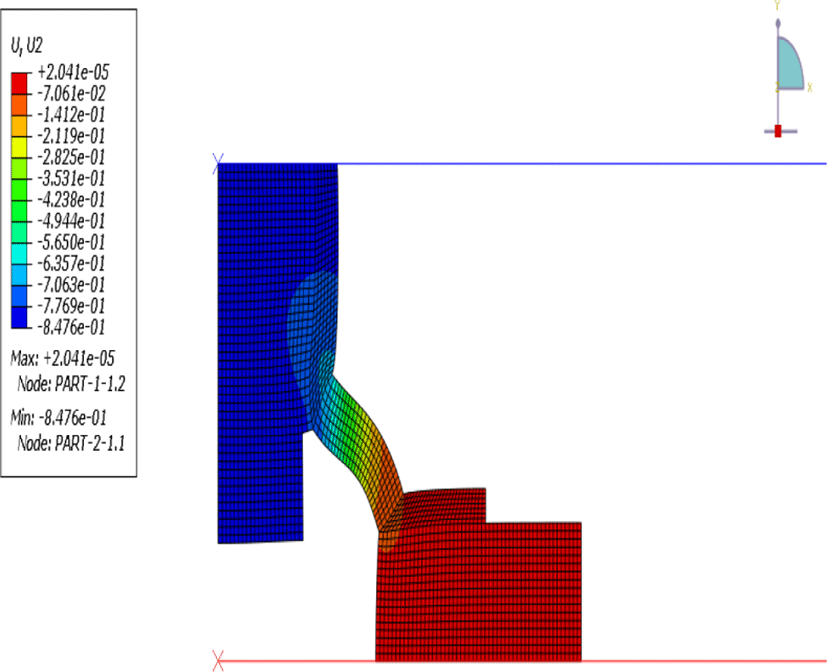
Figure 11과 Figure 12는 조작력 발생 시점과 접촉 발생 시점에서의 Y축 변위의 변화량을 나타낸 그림이다. 고무 스위치 모델의 변화 형상을 조작력 발생 시점과 접촉 발생 시점에서의 고무 스위치 모델의 변화 형상을 파악하고, Y축 변위의 변화량을 산출하는데 유한요소해석 프로그램인 ABAQUS를 사용하였다. Figure 11에서 조작력 발생 시점일 때는 고무 스위치 모델의 변형이 크지 않지만, Figure 12에서 Y축 변위 변화량이 증가하면서 접촉 발생 시점으로 갈수록 모델의 변형이 가속적으로 증가한다는 사실을 확인할 수 있다.
Table 2는 각 노화시험 조건에서 구한 비선형 재료상수를 이용하여 유한요소해석을 통하여 구한 조작력(Pmax, N) 값을 보여준다. 노화일수가 길고 노화 온도가 높을수록 조작력이 감소하는 경향을 보이고 있다. 이는 노화도가 진행됨에 따라 경도와 탄성계수가 감소함으로써 나타나는 현상으로, 일반적으로 노화가 진행됨에 따라 경도와 탄성계수 값이 커지는 천연고무의 특성과 상반된 경향을 보여주고 있다. 2001년 영국의 RAPRA TECHNOLOGY에서 발표한 ‘Ageing of Rubber’ 에서는 여러 종류의 고무 재질에 대한 노화 특성 선도를 제시하고 있다.7 대부분의 고무 재질에서 노화가 진행됨에 따라 경도가 증가하는 경향을 보이고 있지만, 부틸고무, 폴리설파이드 고무 등은 반대의 경향을 보이고 있으며, 실리콘 고무의 경우는 경도나 100% 탄성계수가 크게 변하지 않는 경향을 보여주고 있다. 2016년 한국추진공학회 학술대회논문집에서 발표한 ‘간헐 압축응력완화 시험법을 이용한 불소 실리콘 오링의 수명 예측 연구’ 에서도 열 가속 노화 실험에서 가열 온도가 증가하고 시간이 경과됨에 따라 오링의 강성이 저하되어 기밀력이 감소하는 경향을 보여주고 있다.8
본 연구에서 사용된 실리콘 고무의 경우 노화가 진행됨에 따라 경도 및 탄성계수가 감소하는 경향을 보였다.
Prediction of the Aging Life
Figure 13은 Table 2의 조작력 값의 변화를 노화일수와 노화 온도에 따라 나타낸 선도이다. 노화 시간이 증가하고 노화 온도가 높을수록 조작력 값이 감소함을 알 수 있었다. 150°C에서는 경과일수에 따라 조작력의 변화가 크지 않지만, 240°C 고온의 경우에는 노화 시작 후 7일 이내에서 조작력이 급격하게 감소하는 것을 알 수 있었다. Table 3은 그림 선도로부터 커브피팅하여 구한 각 노화온도에서의 노화일수와 조작력의 관계를 나타낸 수식이다.
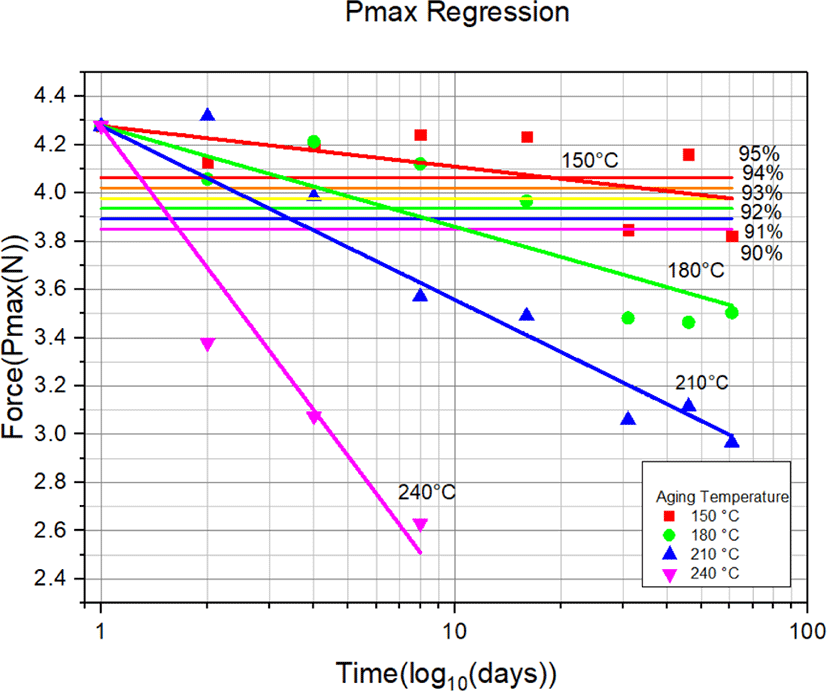
파워 윈도우 스위치에 사용되는 스위치 고무패드 부품의 수명은 고무패드의 조작력(Pmax) 값의 5%~10% 범위 안에서 1%씩 증가하면서 변하는 단계로 간주하고 수명 예측 연구를 진행하였다. 초기 조작력은 4.28N이므로 95%~90% 까지로 변화된 4.06N~3.85N에 도달할 때를 수명으로 간주하였다.
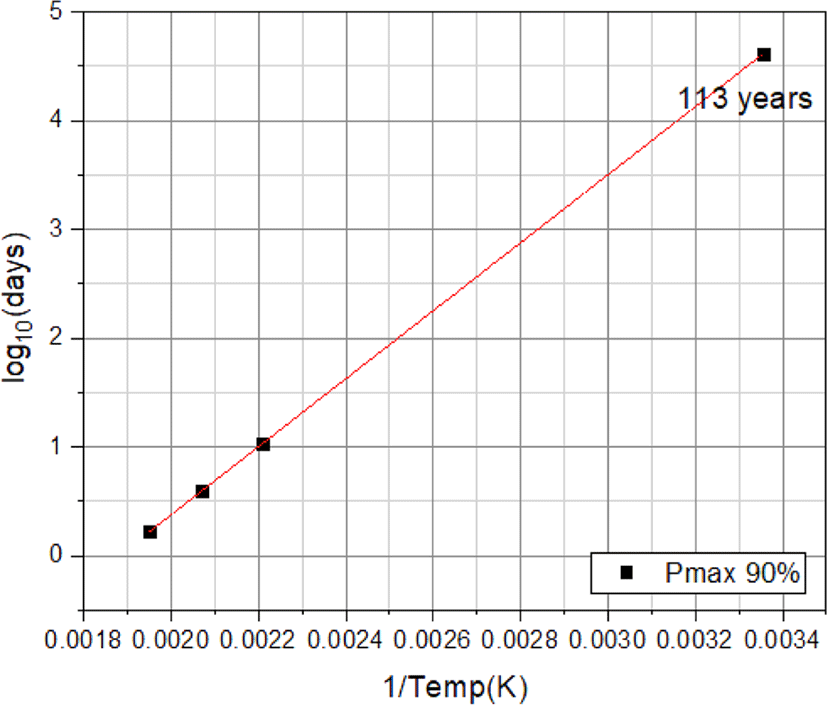
Table 4는 Figure 13의 시험 선도로부터 5%~10% 조작력이 변했을 때의 노화 수명(Aging Life, AL; days)을 아레니우스 선도로 나타낸 관계식이다. Figure 14는 10% 조작력 변화에 대하여 아레니우스 선도 관계식을 산출하여 상온에서의 노화 수명을 외삽법을 통해 산출한 결과 그림이다. 대표적으로 조작력이 10% 변화하였을 때의 수명을 구하는 아레니우스 관계식은 (10) 식과 같다.
여기서, t는 노화시험 온도(°C)이다.
식 (10)으로부터 상온(25°C)에서의 노화 수명은 113년으로 산출된다. 아레니우스 관계 선도로부터 일정 경과시간 후의 조작력 변화율도 산출할 수 있다. 자동차 수명을 20년으로 볼 때 조작력의 변화율은 약 8.4%로써 초기 조작력 대비 10% 이내에 들어 노화에 따른 조작력 변화는 안전하다고 판단할 수 있다.
Table 5는 조작력이 10% 감소한 시점을 해당 부품의 수명으로 간주하였을 때, 각각의 온도(150°C, 180°C, 210°C, 240°C) 조건에서 해당 시편을 노화 시킨 경우를 상온(25°C)에서 해당 시편을 노화 했을 경우와 상호 비교하여 어느 정도의 기간에 해당되는지를 일수로 나타낸 표이다. 이는 조작력이 10% 감소한 시점을 해당 부품의 수명을 간주한 아레니우스 관계식을 활용하여 산출하였다.
| Agint Temperature (°C) | Aging Life Expectancy (days) |
|---|---|
| 2 5°C | 4.13 × 104 days |
| 150 °C | 32.7 days |
| 180 °C | 10.6 days |
| 210 °C | 3.95 days |
| 240 °C | 1.65 days |
위의 95%~90% 조작력 변화를 통해 얻은 각각의 아레니우스 관계식으로 산출한 노화 수명 데이터를 기반으로 조작력 변화-수명 관계 선도로 산출하여 자동차 수명 20년에 적합한 고무 패드 부품의 조작력 변화 상태를 파악하고자 하였다. Table 6과 Figure 15를 보면, 20년을 자동차 수명이라고 간주하였을 때, 해당 고무 패드 부품의 조작력 변화는 8.4% 감소한 것으로 예측되었다.
| Aging life (x, year) | Pmax (y, %) - Aging life (x, year) relationship equation | Pmax (y, %) |
|---|---|---|
| 20 years | Y = -2.17 * log10(x) + 94.5 | 91.6 % |
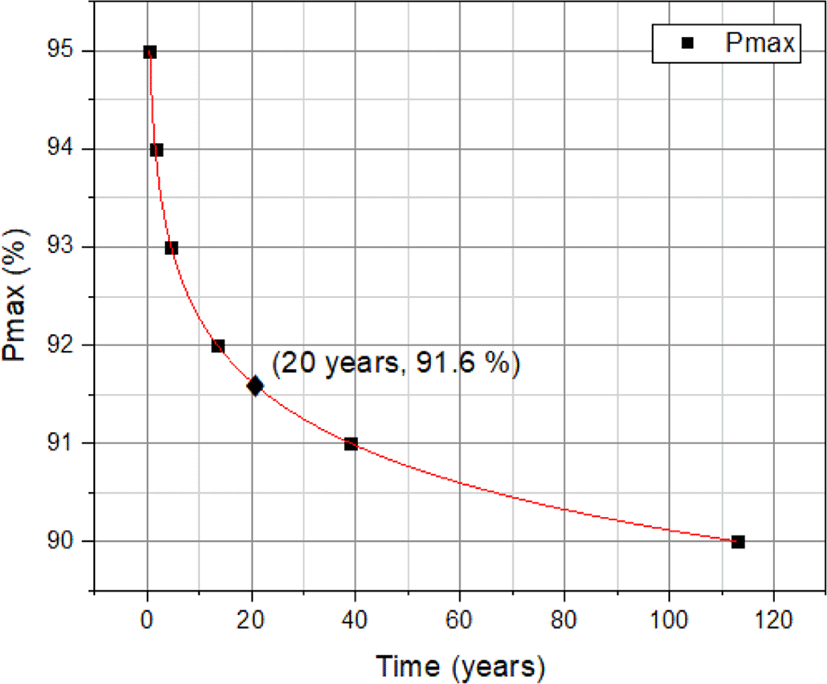
Figure 16은 Table 1의 노화시간 경과에 따른 전단탄성계수 값의 변화를 나타낸 선도이다. 노화시간이 증가하고 노화 온도가 높을수록 전단탄성계수가 감소함을 알 수 있으며, Figure 13의 조작력 변화율과 거의 동일한 경향을 보이고 있다.
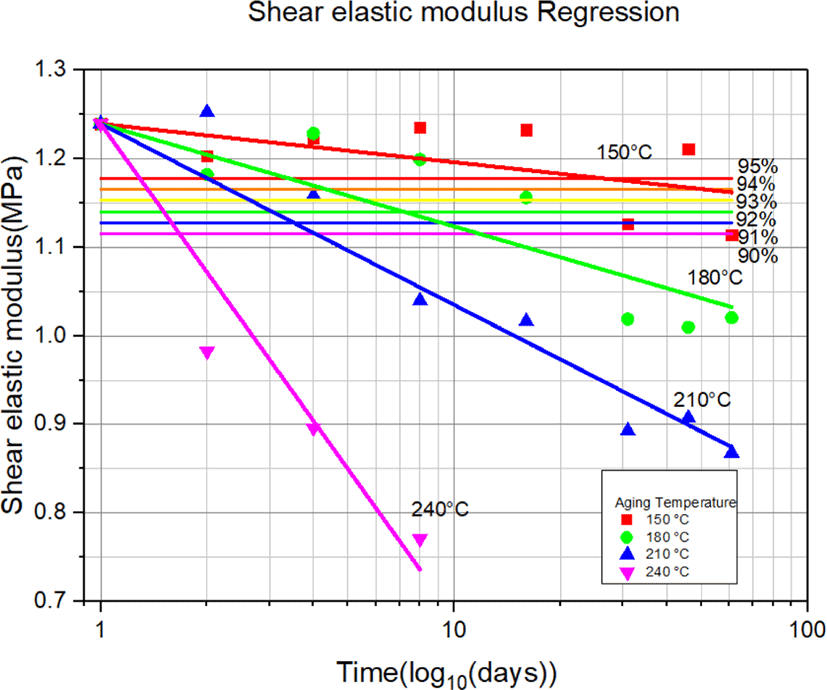
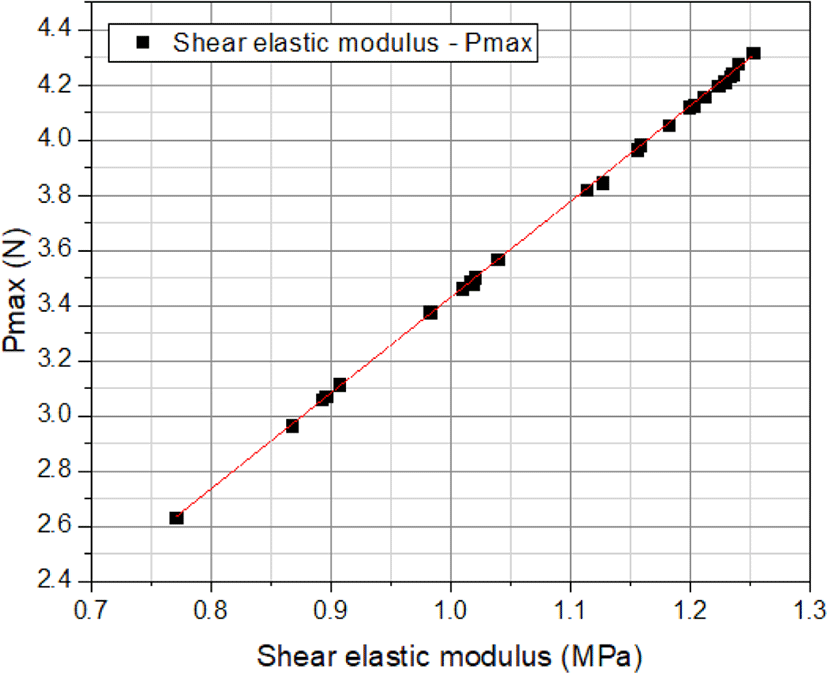
Figure 17은 고무 패드 부품의 각 노화시험 조건에 따른 비선형 재료상수를 이용하여 유한요소 해석한 결과로부터 산출된 조작력 값과 각 노화시험 조건에서의 전단탄성계수 값과의 상관관계를 보여주는 선도이다. 그림에서 보는 바와 같이 조작력의 변화와 전단탄성계수 값의 변화는 선형적인 관계를 보여주고 있으며, 전단탄성계수의 변화로써 노화수명을 예측하여도 큰 문제가 없음을 알 수 있다.
Conclusions
차량용 파워윈도우 스위치 고무패드의 노화수명 예측을 위하여 패드 고무 소재의 가속 열 노화시험을 수행하였으며, 각 노화도에 따른 비선형 재료상수를 구하였다. 구해진 비선형 재료상수를 이용하여 유한요소해석을 수행하여 조작력을 산출하였으며, 노화온도와 노화시간에 따른 아레니우스 선도를 유도하여 다음의 결론을 얻었다.
노화온도는 150°C, 180°C, 210°C, 240°C의 4가지 조건에서 1~60일까지 노화시험을 수행하였다. 고무패드의 조작력 값이 초기 값 대비 10% 변화되었을 때를 수명으로 간주할 때 자동차의 수명보다 훨씬 긴 113년으로 예상되어 노화수명은 충분히 안전함을 알 수 있다.
자동차의 수명을 20년으로 볼 때 고무패드의 조작력 변화율은 약 8.4%로써 초기 조작력 대비 10% 이내에 들어 노화에 따른 조작력 변화는 안전하다고 볼 수 있다.
각 노화시험 조건에서의 전단탄성계수 값과 유한요소 해석한 결과로부터 산출된 조작력과의 상관관계를 살펴 본 결과 조작력의 변화와 전단탄성계수 값의 변화는 선형적인 관계를 보여주고 있으며, 전단탄성계수의 변화로써 노화수명을 예측할 수 있음을 알았다.
본 연구를 통해 차량용 파워윈도우 스위치 고무패드 부품의 노화수명을 예측할 수 있는 방법이 제시되었다.