Introduction
압출공정은 장시간 동안 압출물을 토출하여 필름 또는 시트를 만들기 때문에 압출물의 균일성을 지속적으로 유지시켜야 한다. 그리고 생산 공정에서 생산성을 확보하기 위해서 토출량을 예측하는 것이 중요하다. 또한 압출기에 과부하가 가해지지 않는 운영 조건에 대한 데이터 확보가 가장 중요하다. 압출 스크류 및 다이 내 유동에 관한 연구는 그 복잡한 유동 현상과 비선형성으로 인하여 준 경험적 방법에 많이 의존해 왔다. 그러나 압출 다이 내의 유동은 최종 생산된 제품의 품질 및 공정의 생산성과 직접적인 관련이 있으므로 다이 최적 설계차원에서 많은 연구가 시도되고 있다.1,2,3
다이특성과 스크류특성은 압출공정에서 매우 중요한데, 스크류나 다이의 내부 유동이나 압력등을 확인 할 수 없으므로 여러 번의 실험을 거쳐 공정조건을 찾아왔으나 시뮬레이션을 통하여 스크류의 회전속도에 따라 유량과 압력그래프의 변화, 그리고 스크류 회전속도에 따라 다이에서 나오는 토출량의 변화에 대한 경향성을 확인 할 수 있어 공정 조건에 대한 데이터 베이스를 구축하여 생산성 향상에 큰 도움을 줄 수 있다. 김시조 외 1명은 압출기 내에서의 스크류 특성에 관하여 3차원 비뉴턴유체에 대하여 3차원 유동효과를 관찰하였고 전체 형 상계수의 단면 종횡비에 따른 변화율이 단면 종횡비에 대하여 관계없이 일정하다라는 것을 알아내었다.2
압출물을 균일하게 생산하기 위해서는 다이 출구의 속도 분포가 중요한 역할을 한다. 다이 출구의 속도 분포는 다이 형태 뿐 만 아니라 스크류의 형태에 따라서 변화가 나타나기 때문에 압출 공정에서 안정적으로 압출물을 균일하게 유지시키며 토출량을 예측하기 위해서 스크류 특성 다이 특성 해석 뿐 만 아니라 다이 최적 설계 연구도 많이 진행되어 왔다. A. W. Birley외 2명은 싱글스크류와 다이에 대하여 각각의 특성 곡선을 하나의 그래프에 나타내어 설명하였다.4 다양한 압출 제 품 형상을 얻기 위한 전산 최적 해석, 튜브, 쉬트, 필름, 타이 어 트래드 압출을 위한 최적 다이 형상 설계가 필요하다. 다이 전산 설계 기술의 참고서적으로 Walter Michaeli의 대표적인 서적이 있으며 가장 오래된 압출 다이 설계 기술의 표준 서로 알려져 있다.5 다이 설계에서 다이 특성을 이해하고 유동 패턴을 전산설계하여 최종적으로 단면에 걸쳐 균일한 속도로 최적설계 하여야 한다. 이러한 속도 분포가 나오지 않으면 다양한 속도를 수용하기 위해 원하는 모양에서 왜곡된다.6
필름캐스팅은 용융된 필름을 다이를 통해 압출하고 롤에 의하여 연신시켜 최종적으로 제품의 폭과 두께를 조절하는 공정이며 필름을 빠르게 생산하기 위한 방법이다. 본 연구에서는 전산수치모사를 위하여 Polyflow7 상용소프트웨어를 사용 한다. 이 소프트웨어는 점성 및 점탄성이 주요한 영향을 미치 는 복잡한 고분자 재료 가공의 전산모사 분야에 널리 사용되 는 소프트웨어이다. 본 연구에서 사용된 형상은 필름압출공 정에서 주로 사용되는 일반적인 T-die를 사용하여 형상 축소 하여 스케일 효과를 관찰한다. 또한 키이홀다이(keyhole die), LTCD (linear tapper coathanger die), CTCD (curved tapper coathanger die)의 다이 3종에 대하여 3차원으로 모델링하여 다이 형상 변화와 파워모델지수(power-law model index)에 따른 다이 특성 변화를 비교하였다. 파원모델 지수를 관찰하기 위해 폴리머 재료인 PMMA (Poly methyl methacrylate)에 Nanoclay 5 wt%를 첨가한 PMMA-5 재료를 참고하며,8 다이 특성에서는 각각의 공정 변수에 따라 내부 유동을 분석하고 다이 크기에 따른 다이 특성의 변화를 관찰한다. 또한 Keyhole, LTCD, CTCD의 다이 3종에 대하여 점성 모델로 유량을 변화시켜 3개 다이의 유동 및 출구 속도 프로파일을 관찰한다. 또한 LTCD 다이에서 파워모델지수를 변경하여 다이 와 파워모델지수에 따른 유동의 차이를 분석하고 파워모델지 수의 변경에 따른 다이특성을 관찰한다. 본 연구의 최종 목표는 전체 압출기에서의 수치 해석, 필름 압출 공정에서 최적의 금형 설계를 위해 금형 출구에서 균일한 속도 분포를 나타 내는 다이 형상 최적화이다.
Governing Equations
질량보존의 법칙(Mass conservation law)은 다음과 같이 표 현된다.
만약 밀도 ρ가 일정한 비압축성 유체인 경우 연속 방정식은 아래와 같이 정리된다.
모든 물체에 대하여 작용하는 힘의 균형으로부터 얻은 식을 운동량 방정식이라고 하며 아래와 같이 표현되어 진다.
는 체력(Body force), 는 전체 응력으로 아래와 같이 점 탄성 모델의 구성방정식에 따라 결정되며, 여기서 는 점탄성 영역의 응력, 는 점성영역의 응력이다.
고분자 용융체는 뉴턴 유체(Newtonian fluid)가 아니며 일반화된 뉴턴 유체(generalized Newtonian fluid)이다. 본 연구 에서는 점탄성 모델 대신, 일반화된 뉴턴 점성 모델을 사용하 였다. 다이특성 해석에 사용된 점성 모델은 Bird-Carreau 모델이며 아래 식으로 나타낸다.
여기서 η∞ 은 infinite-shear rate viscosity이며, η0은 zero-shear rate 점도이고, λ는 완화시간(natural time)으로 유체가 뉴턴유체에서 power law 거동으로 바뀌는 전단 속도의 역수이다. n 은 power law 지수(index)를 나타낸다. 이 때 n = 1이면 점도 그래프의 기울기가 0이 되고 결국 점도가 일정한 뉴턴 점도를 나타나게 된다.
Screw and Die Characteristics
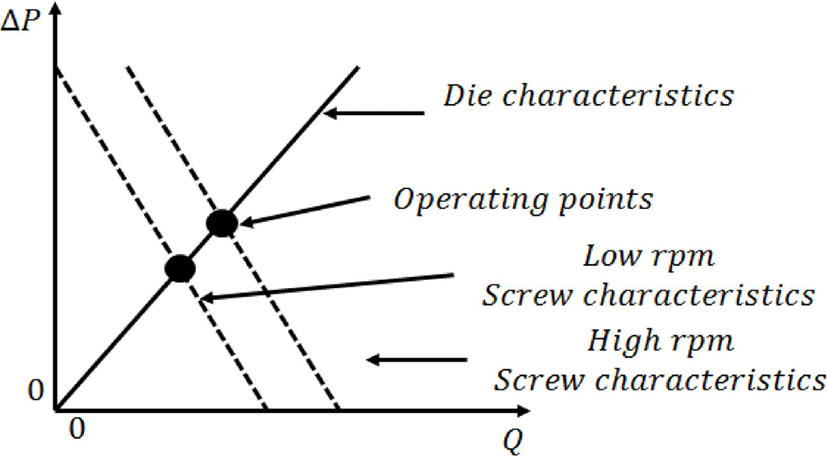
다이 특성과 스크류특성은 공정상에서 최적의 공정을 찾아 내는 지표이기도 하며 스크류 헤드부 즉, 다이 입구에서 걸리는 높은 압력으로 인한 사고를 방지 할 수도 있다. 또한 실험을 통하지 않고도 스크류의 회전속도에 따른 다이에서의 토출량을 확인 할 수 있다. 스크류 특성은 같은 역압력(back pressure) 하에서 회전속도가 증가할수록 토출량이 증가하고 동일한 회전속도에서 역압력이 증가할수록 토출량은 적어지 는 그래프가 나타난다. 다이특성은 입구에서 들어오는 유량이 증가할수록 다이 입구에서 압력이 점점 높아지는 그래프가 나타나게 된다. 이 그래프들을 하나의 그래프로 나타낸 것 이 Figure 1이며 다이특성과 스크류특성을 그려봄으로써 각 각의 공정 조건을 확인 할 수 있다. 공정조건들은 스크류 회전속도, 스크류 헤드부분에 작용하는 역압력, 그리고 다이 입구로 들어오는 유량들의 조건들을 확인하여 스크류 회전속도에 따른 토출량을 확인 할 수 있게 되고 공정을 개선할 수 있게 된다.
Numerical Simulation
수치해석에서는 형상에 대한 모델링과 경계조건 및 물성치 등을 제대로 입력하는 것이 중요하다. 현상에 대한 값이 다르게 입력된다면 실제 현상과 다른 결과 값을 도출하게 되며 이는 심각한 문제를 초래 할 수 있다.
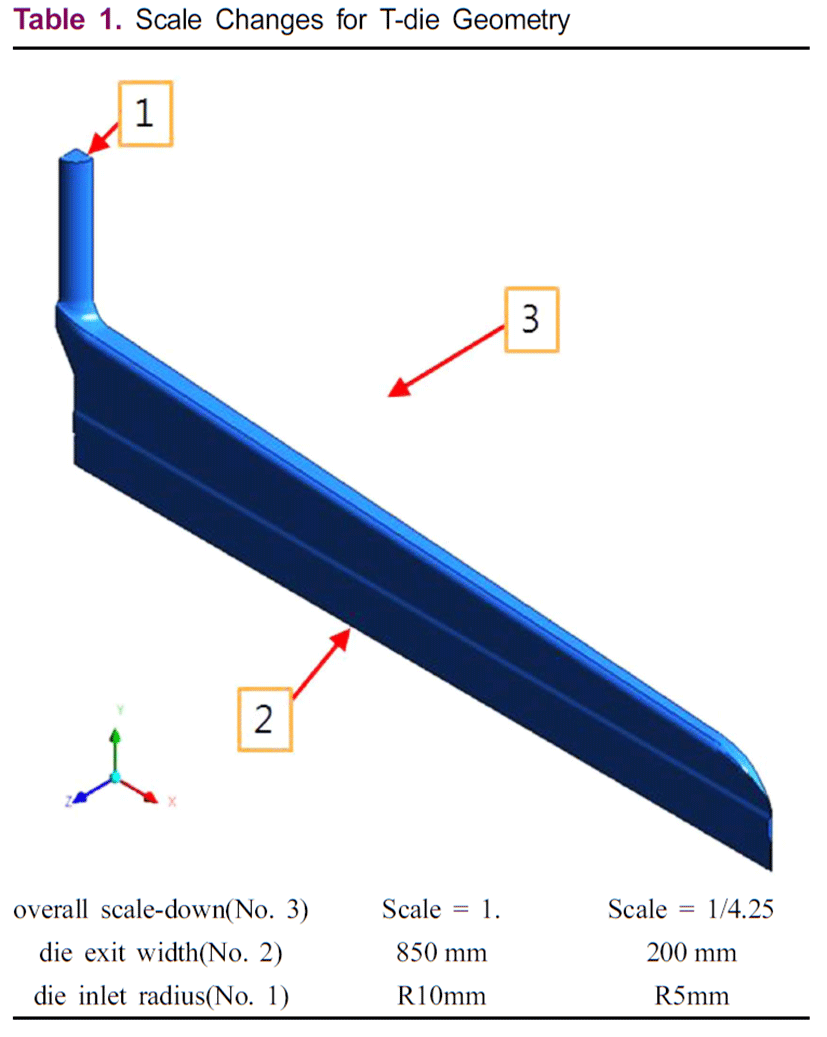
본 연구에서 사용된 형상은 필름압출공정에서 주로 사용되는 일반적인 T-die를 사용하여 형상 축소하여 스케일 효과를 관찰한다. 다이 크기에 대하여 그 영향을 확인하기 위해 다이의 스케일을 줄여 제작하였으며 구체적인 3차원 치수 스케일 값은 Table 1에 나타내었다. 전체 형상 축소는 Table 1의 3번 처럼 원본을 1/4.25 Scale로 축소하였고, 다이 출구 폭은 Table 1의 2번처럼 850 mm에서 200 mm, 다이 입구 반지름은 Table 1의 1번처럼 반경 R10mm에서 R5mm로 변경되었으며, 다이 출구 두께는 1.5 mm에서 0.25 m로 변경되었다. 그 외의 형상 정보는 다이 출구 폭에 맞춰 1/4.25 Scale로 조정되었다.
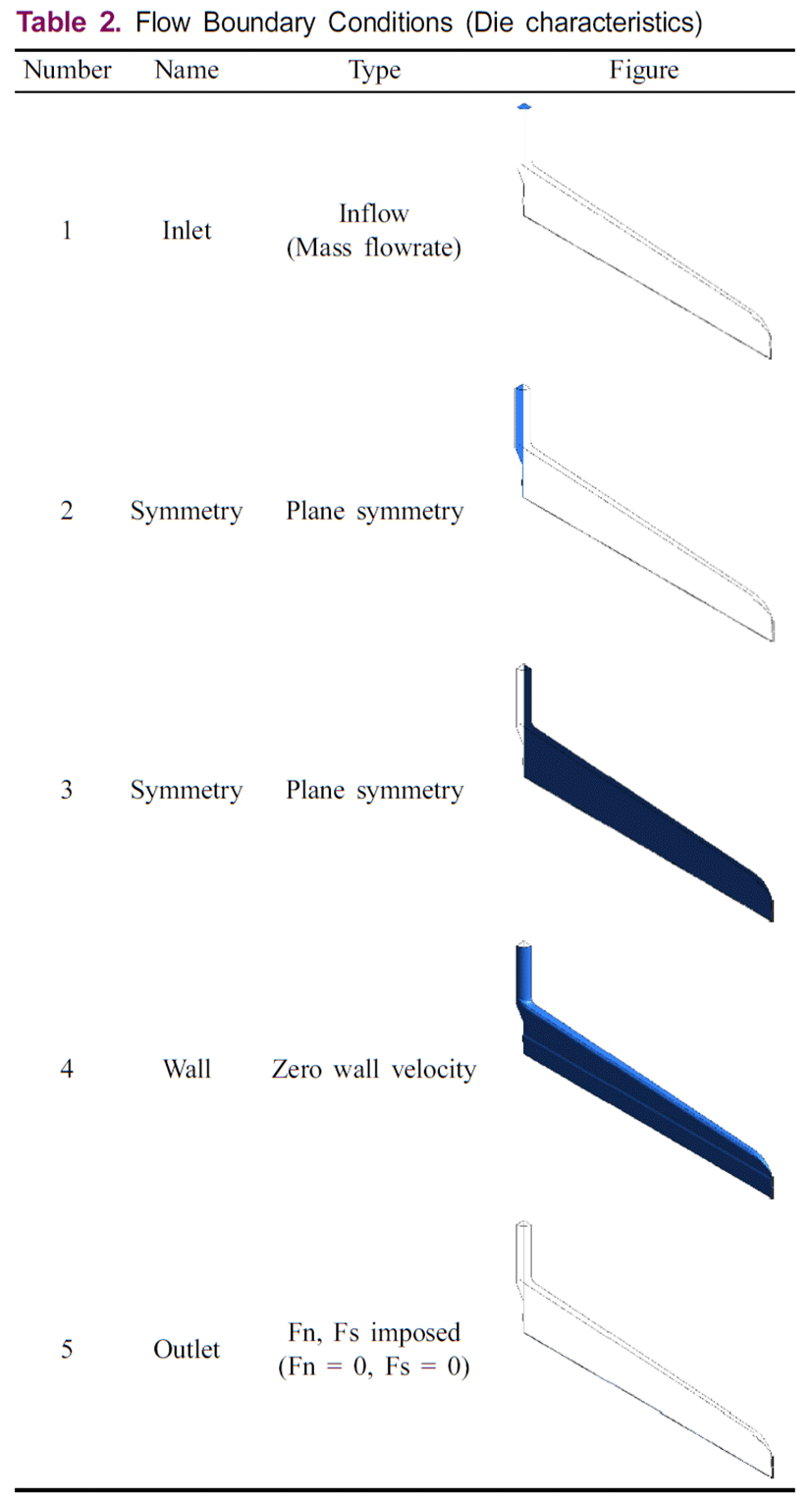
경계조건은 Table 2에 정리하였다. 경계조건에서의 Inflow 값, 즉 번호 1번 Inlet 경계에서 질량 유량을, 번호 2와 3에서 대칭 조건, 번호 5에서 출구 조건을 부여하였다.
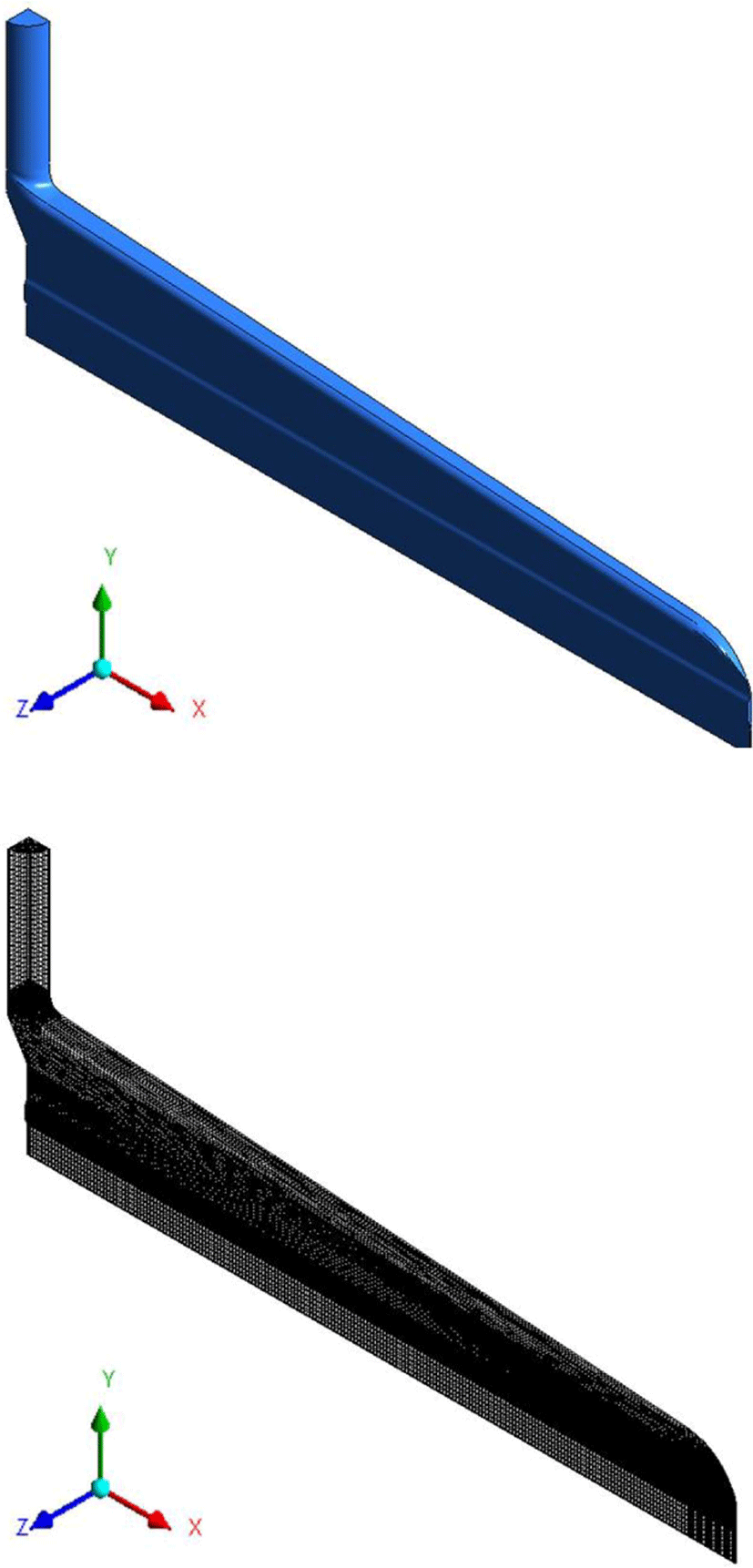
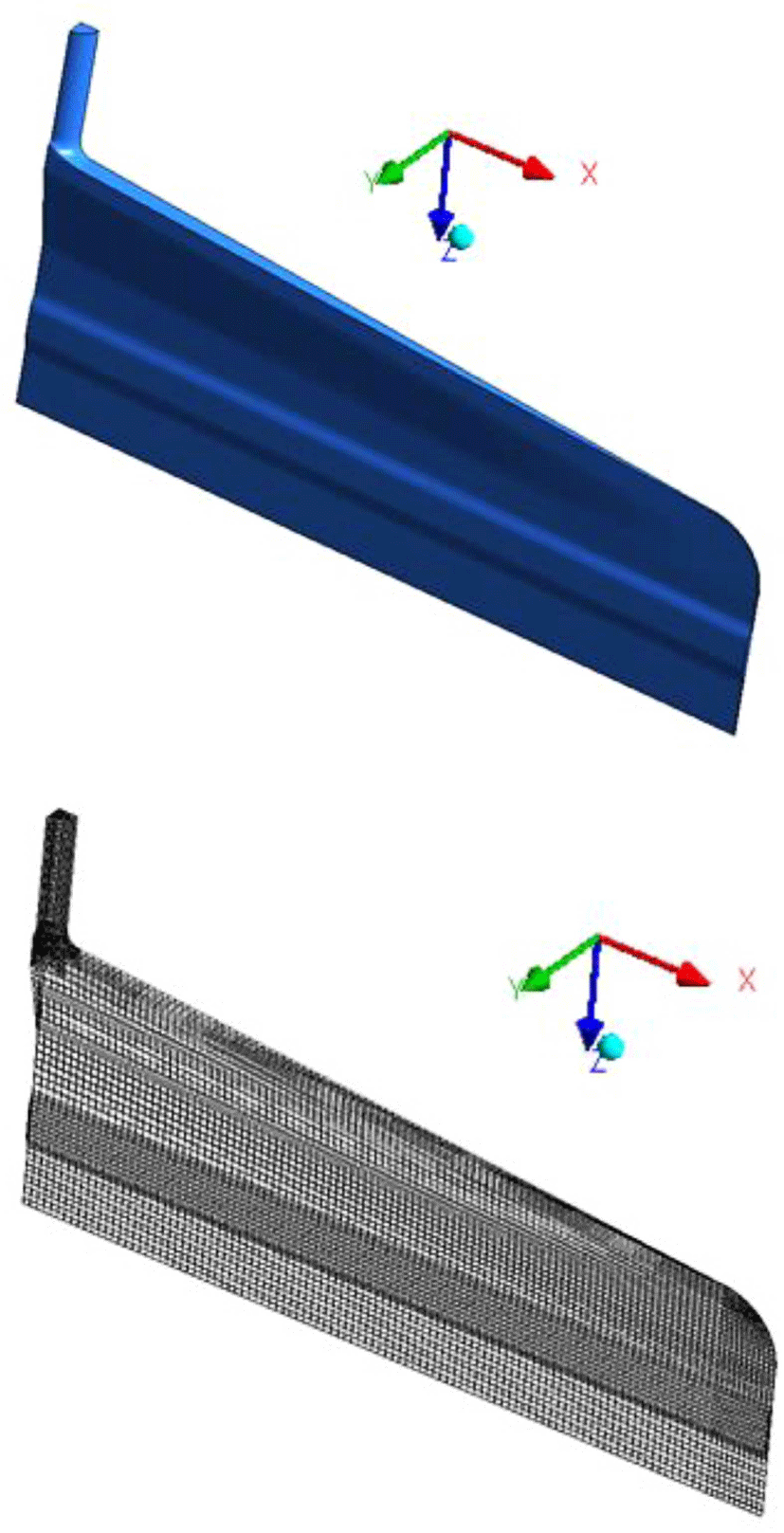
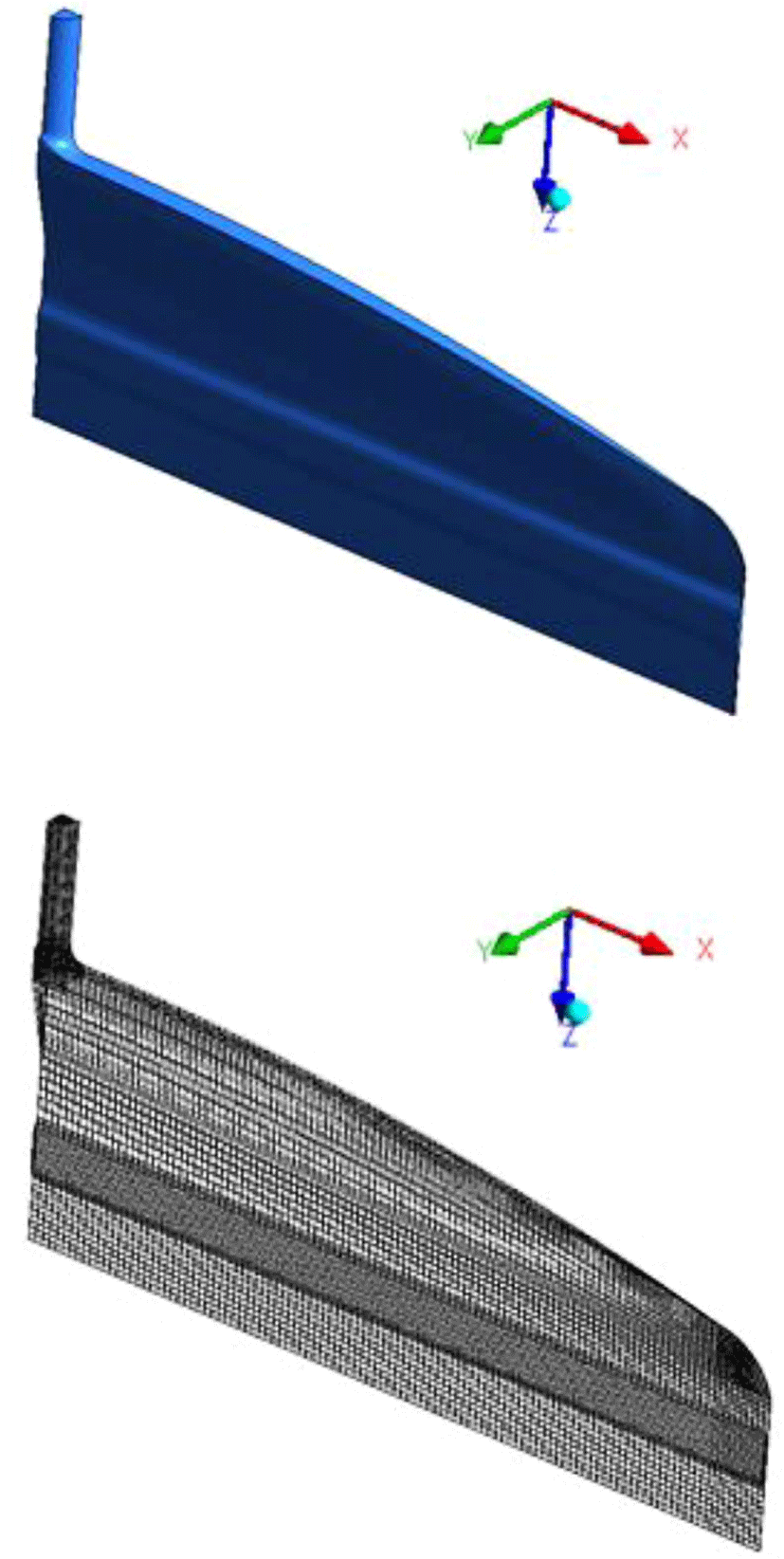
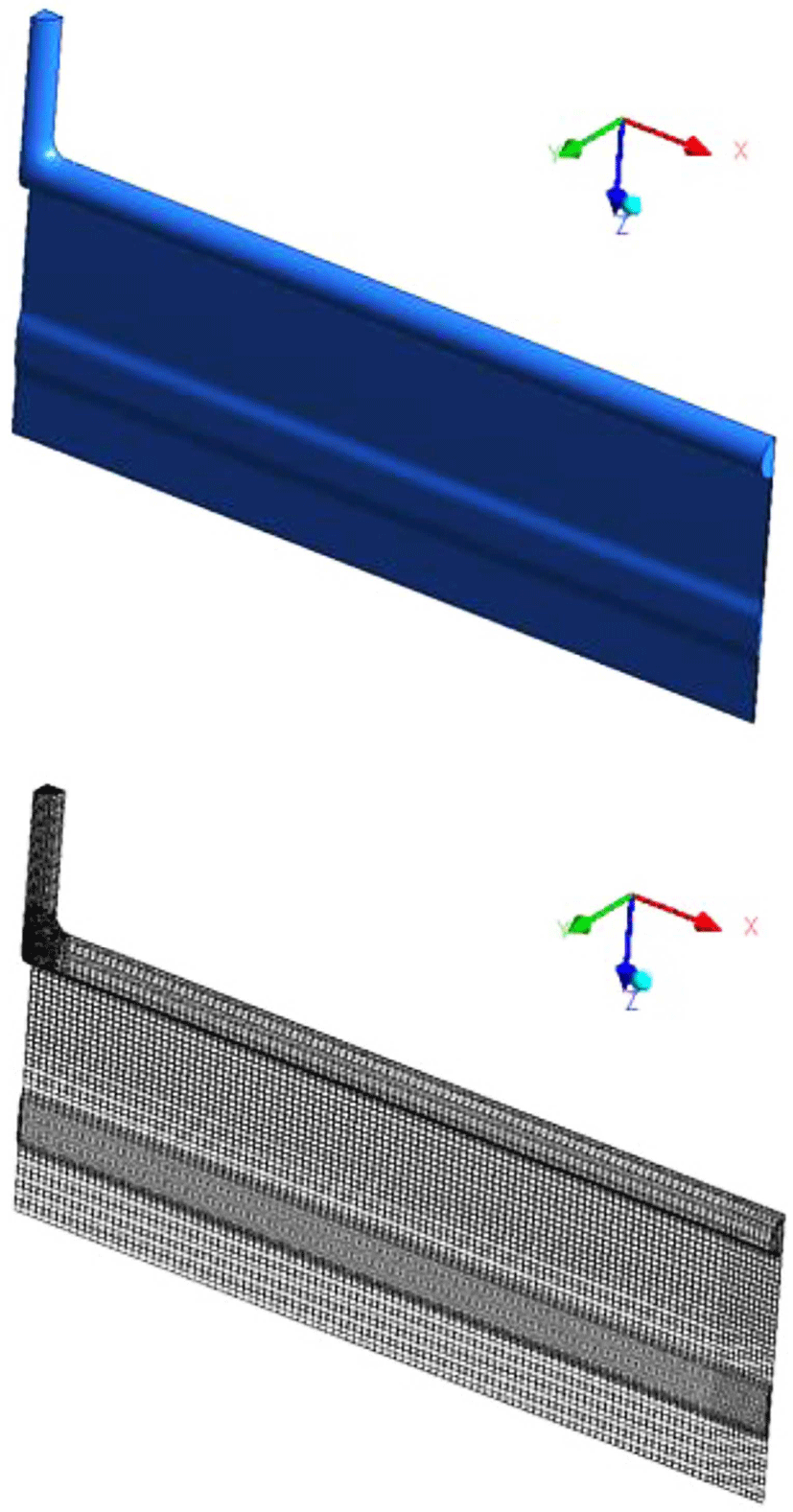
T-die의 형상과 격자를 Figure 2에 나타내었고, 다이특성에 관하여 변경되는 인수 값은 Boundary 1의 질량유량값이며 1/ 4형상 기준으로 실제 입력 값은 12.5, 25, 50, 65, 80, 100, 115.8 g/s이고 전체형상을 기준으로 하였을 경우 50, 100, 200, 260, 320, 400, 463.4 g/s에 대하여 해석을 진행하였다.
일반적인 T-die를 변형한 대표적인 다이, 즉 LTCD, CTCD, Keyhole 다이에 대하여 파워모델지수에 따른 영향 분석 및 각 각의 다이에 대한 형상의 변화에 따른 유동분석을 실시하기 위하여 3종의 다이형상을 제작하였다. LTCD의 형상과 격자 를 Figure 3에 나타내었고, CTCD의 형상과 격자를 Figure 4 에 나타내었으며, Figure 5에는 Keyhole 다이의 형상을 나타 내었다. Flow boundary condition은 Table 1과 동일하며 1/4형 상 기준으로 Inflow에 각각 1.25(g/s), 2.5(g/s), 3.75(g/s)을 Input값으로 주었다. 전체형상 기준으로는 이 값들을 4배하면 각각 5(g/s), 10(g/s), 15(g/s)가 된다.
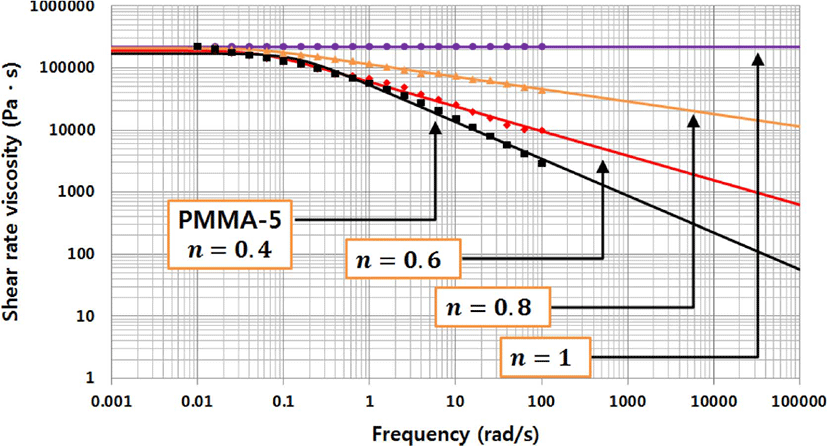
Figure 6에는 유변학적 물성 데이타를 Bird-Carreau 모델로 피팅한 결과를 파워모델지수에 따라 변화된 결과를 하나의 그 래프로 나타내었다. Figure 6에서 실선은 식 (5)에 피팅한 결 과를 나타낸다. 본 연구에서는 파워모델지수에 따라 영향을 수치해석 및 그 결과를 분석하고, 또한 다이 3종에 대하여 n=0.6인 경우의 데이터를 사용하여 해석을 진행하였다.
Numerical Results and Discussion
다이특성에서는 다이 입구에 작용하는 압력, 유량도 중요하 지만, 다이 내부 유동은 다이 출구에서의 유속에 영향을 끼치기 때문에 매우 중요하다. 다이 내부에서 유속은 다이 입구에서 빠르게 들어오면서 첫번째 메니폴드(first manifold)에서 속도를 폭 방향으로 점차 균일하게 안정화가 이루어지고 두번째 메니폴드(secondary manifold)에서는 출구방향으로 나가면서 다이 내부 유속이 균일하게 안정화가 되어진다.
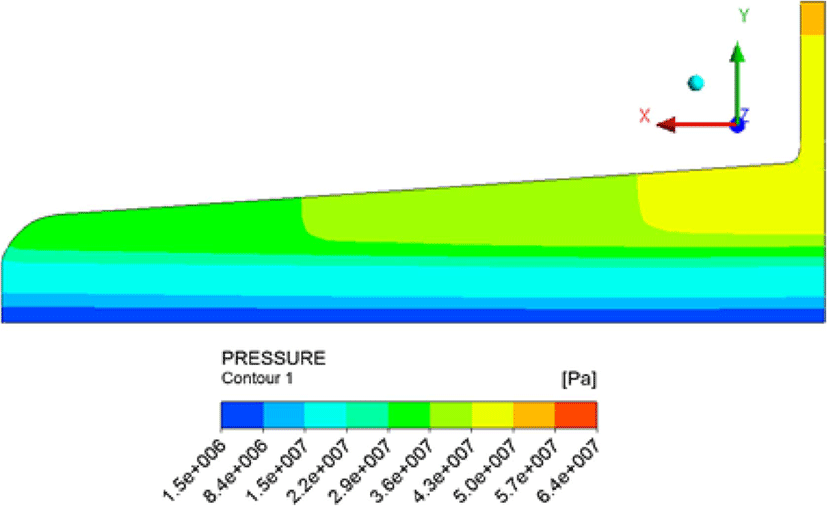
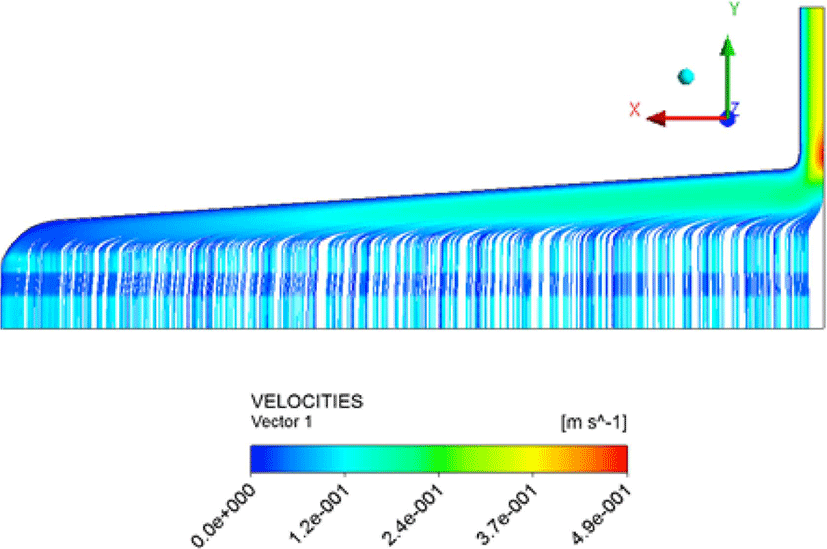
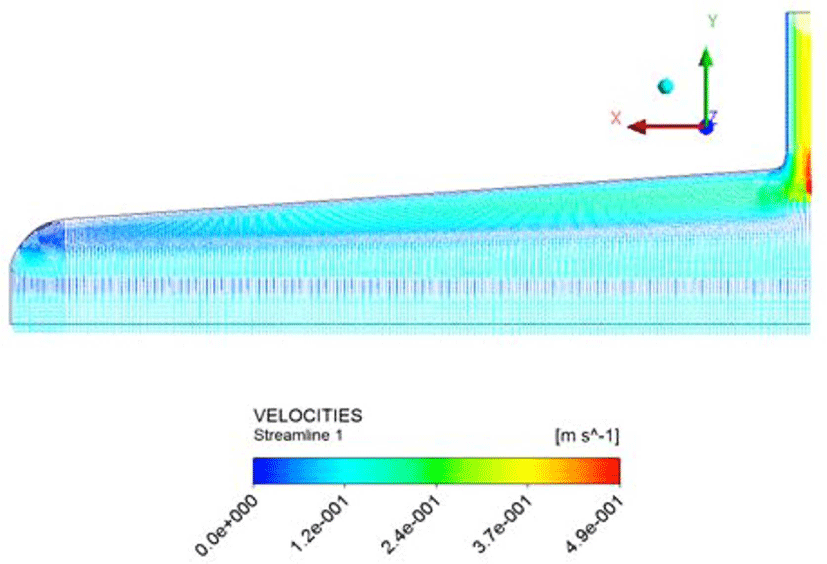
Figure 7, 8, 9는 질량유량 115.8(g/s)에서의 결과를 나타낸 것으로 다이 내부의 변화를 확인하기 위하여 각각 압력 등고선, 유선, 속도 벡터장을 다이 대칭면에서 관찰하여 나타낸 것이다. Figure 7은 입구 부분에서 압력이 가장 높게 나타나고 첫번째 메니폴드에서 압력의 균일한 분포 변화가 이루어지게 되면서 다이 출구 방향으로 안정화가 이루어지게 된다. Figure 8, 9는 유동이 도중에 꼬이거나 와류(Vortex)가 생기지 않고 첫 번째 메니폴드에서 다이 벽면을 따라 유속의 안정화가 이루 어지는 모습을 확인되었으며 두번째 메니폴드에서는 출구방 향으로 유속이 안정화되어 출구로 빠져나가는 모습을 확인하 였다.
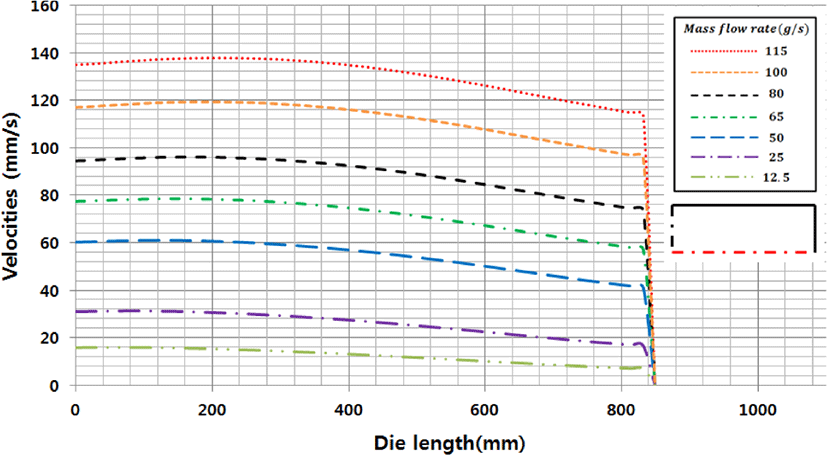
Figure 10은 폭 방향으로는 등속 일정유량으로 빠져나오는지 알아보기 위해, 다이 출구의 폭 방향과 두께 방향으로 속도를 측정하여 나타내었다. Figure 11은 다이 출구에서의 유속을 두께 방향으로 나타낸 그림이다. 두께방향의 원점은 출구 단면의 중앙점을 선택하였다. 속도 분포는 포물선 모양으로, 각 입력 질량유량 값에 따라서 변화하는 속도 분포를 하나의 그래프에 나타내었다. 벽면 조건을 zero wall velocity로 주어졌으므로 두 종류의 그래프 모두 벽면에서는 속도가 0이 었으며 두께방향으로는 포물선 형태로 질량유량이 증가함에 따라 증가함을 알 수 있다. 폭 방향으로는 균일한 유동이 이루어지고 있으나 질량 유량이 증가함에 따라 균일한 속도장 형성이 잘 이루어 지지 않음을 알 수 있다. 두 방향 모두 중앙 부분이 유속이 가장 빠른 포물선 형태가 나오는 것을 확인할 수 있으나, 질량유량이 증가함에 따라 폭방향으로 속도 가 최대가 되는 부분이 중심에서 점점 멀리 이동하는 경향을 보인다.
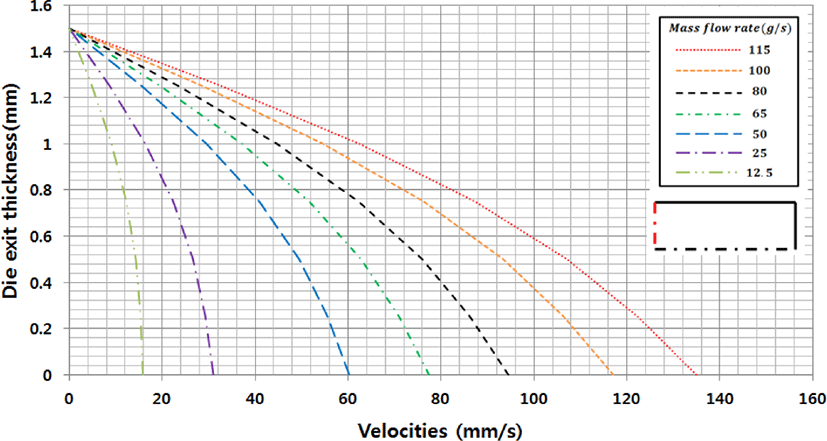
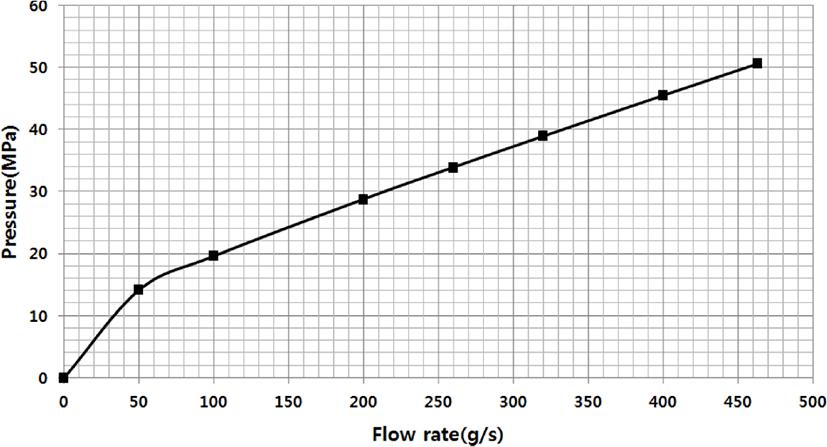
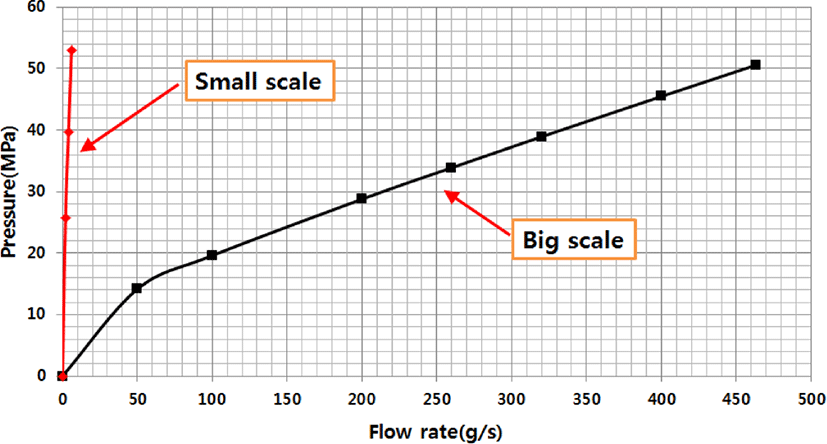
Figure 12는 실제 스케일(big scale) T-Die 특성 곡선 그래프를 나타낸 것이며 x축은 입구의 Mass flowrate (g/s)이며, 이때 질량유량값은 전체 다이 형상 단면에서의 질량유량으로 나 타내었다. y축은 입구의 pressure (MPa)이다. 온도 영향을 고려하지 않는 등온 조건으로 해석하였지만 전단담화(shear thinning) 현상으로 인하여 곡선형태 증가가 50(g/s)에서 둔화하는 현상이 나타났다. 다이 형상 스케일 크기 변화에 대하여, 즉 축소 모델에 대한 압력 및 유동장에 관하여 조사한 결과 Figure 7, 8, 9의 결과와 유사하였다. 또한 다이 출구의 폭 방향과 두께 방향으로 속도를 측정하여 조사한 결과도 Figure 10, 11의 결과 분석과 유사하였다.
Figure 13은 Figure 12에 나타낸 실제 스케일(big scale) T-die의 특성곡선을 축소 형상(small scale) 모델의 다이특성과 함께 하나의 그래프에 나타낸 것으로 축소 모델에 대한 스케일 차이에 따른 다이특성의 차이를 뚜렷하게 나타낸다. 다이 형상이 형상 스케일로 인해 줄어들수록 적은 유량에도 큰 압력이 나타나는 것을 확인 할 수 있으며 이는 다이 크기에 따라 입력 유량값을 제대로 주지 못할 경우, 즉 스크류 회전속도를 어떤 한계를 넘어설 경우, 다이 내부 압력 증가가 현저해서 다이의 변형 혹은 파손을 불러 일으킬 수 있음을 의미한다.
Figure 14, 15, 16은 LTCD, CTCD, Keyhole die의 3가지 종 류에 대하여 1/4 Geometry기준 질량유량 1.25(g/s), 파워모델 지수 0.6인 경우의 결과이다. Figure 14에서 다이 입구에서 압력이 가장 높게 나타나는 다이는 Keyhole die이며 다른 다이 와 비교하였을 때, 약 15MPa가량 차이가 나는 것을 확인 할 수 있다. Figure 15, 16은 3가지 다이에 대한 유선과 속도장 분포이며, 각 다이에 대하여 속도분포는 많은 차이가 나지 않 음을 확인 할 수 있다. 유선상에서 유동을 확인한 결과 유동 분포가 가장 좋은 것은 CTCD인 것을 확인 할 수 있다. LTCD 와 Keyhole die의 경우 입구에서부터 들어오는 유동이 다이의 끝까지 유동이 흐르지 않는 것을 확인 할 수 있으며, LTCD 의 경우엔 첫번째 메니폴드 길이가 작고 기울기가 커지면 CTCD와 같은 유동을 보일 수 있으나 같은 형상의 첫번째 메니폴드 길이에 대하여 CTCD가 더 좋은 효율을 보인다. Keyhole die의 경우 다이의 끝 부분을 완곡하게 Round를 주어 다이를 가공하면 더 좋은 결과를 보일 수 있을 것으로 예측된다.
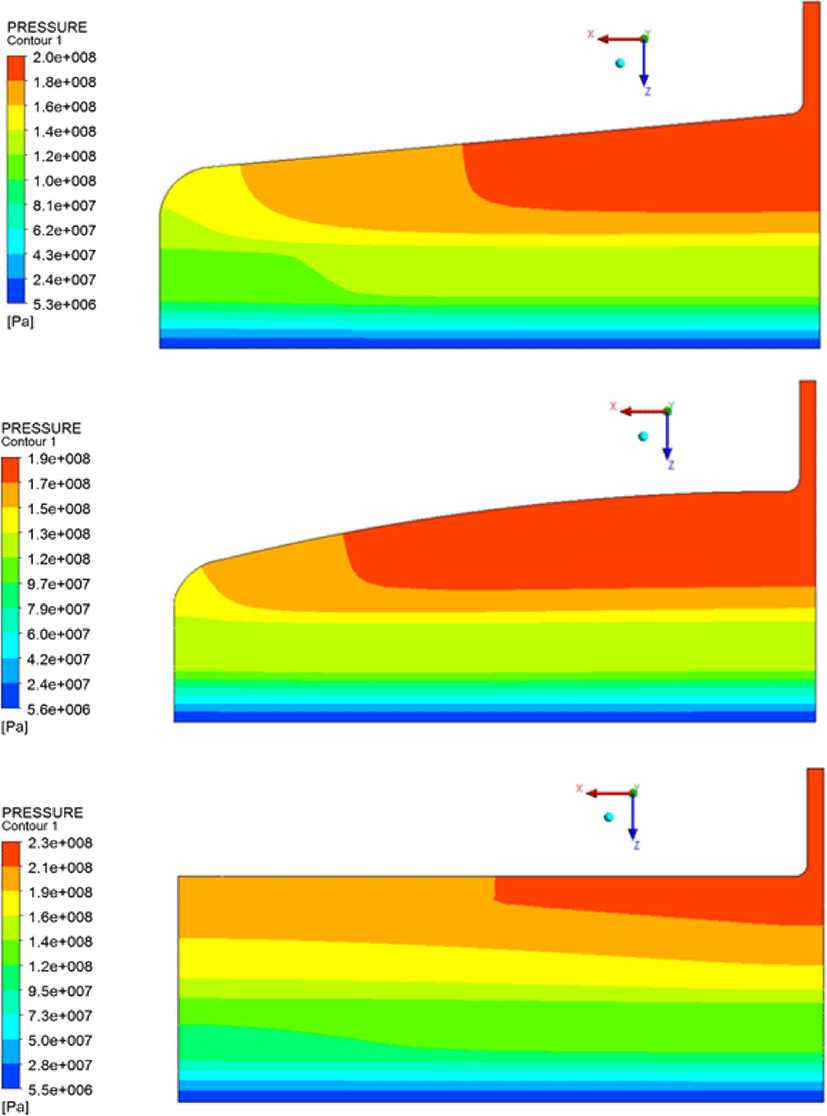
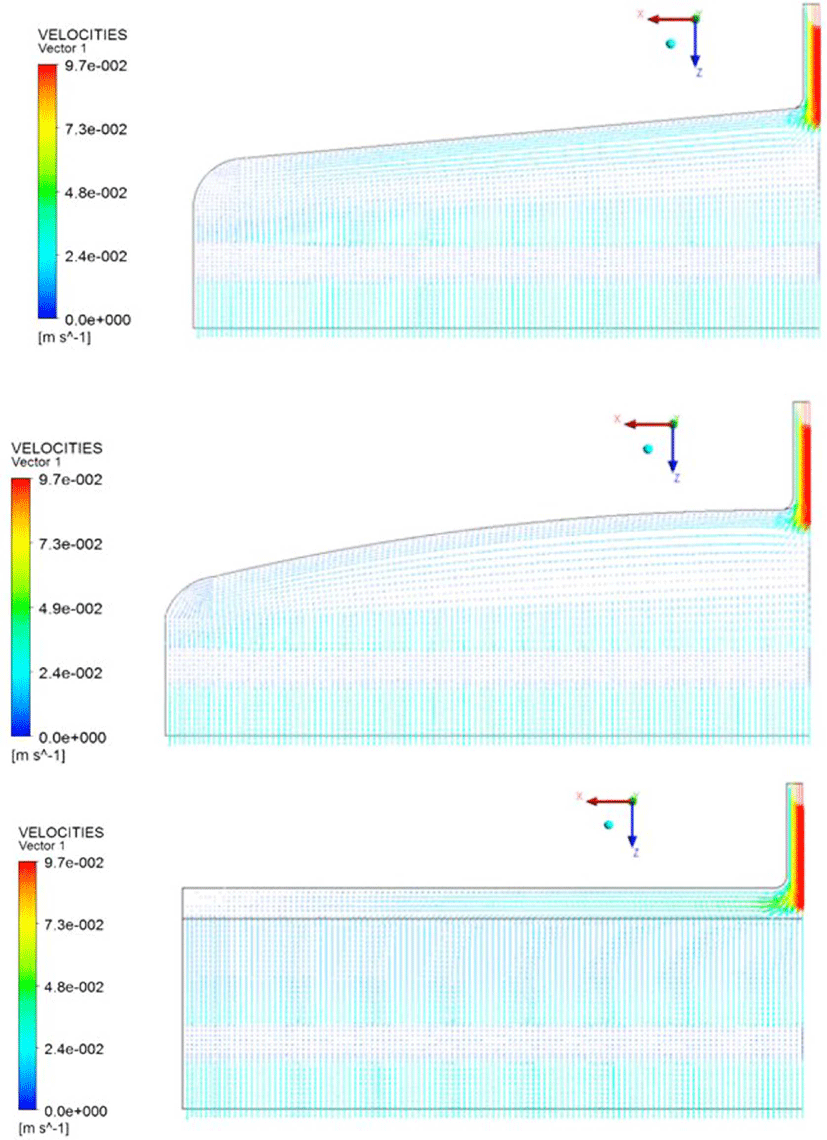
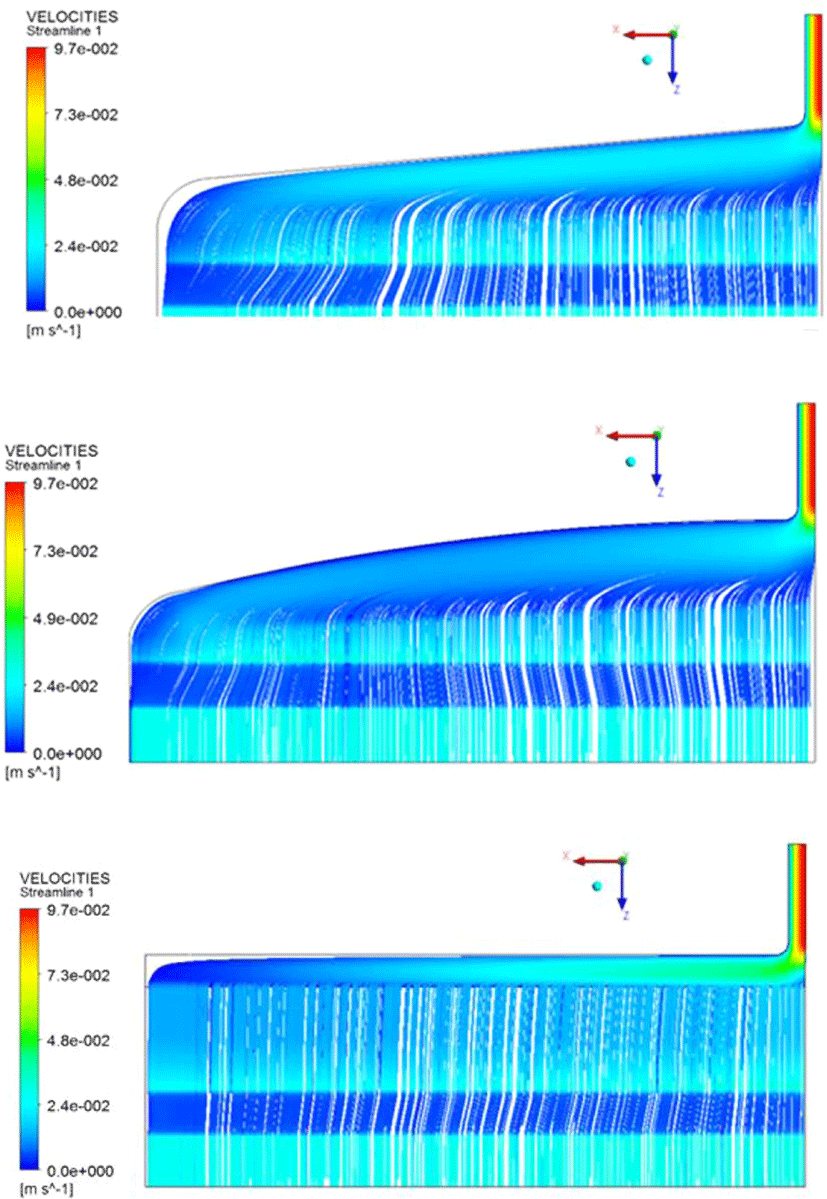
Figure 17, 18은 LTCD, CTCD, Keyhole die의 3가지 다이 에 대하여 출구에서의 속도분포를 각 질량유량에 대하여 폭 방향과 두께 방향으로 하나의 그래프에 그려낸 것이다. Figure 17에서 LTCD, Keyhole die는 균일한 속도분포 형태를 나타 내지만 CTCD의 경우 중앙 부분이 속도가 낮게 나오는 형태 를 보이면서 폭 방향 끝으로 진행하면서 다른 다이 보다 높은 속도를 나타내고 LTCD의 경우 폭 방향 끝으로 진행하면서 다른 다이 보다 속도의 감소율이 커진다.
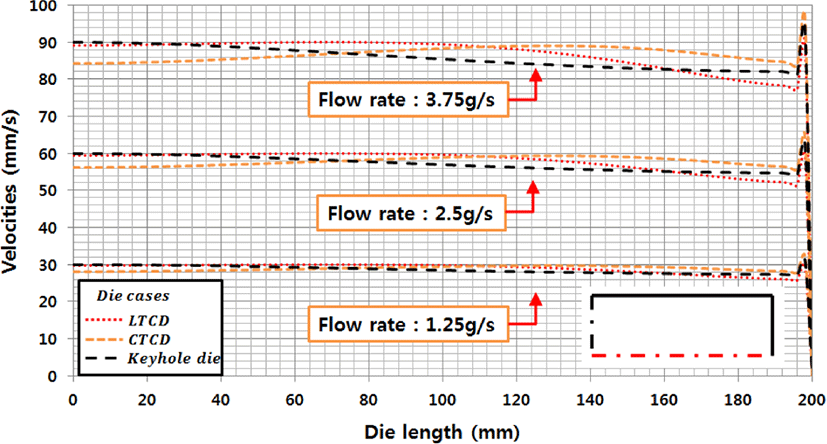
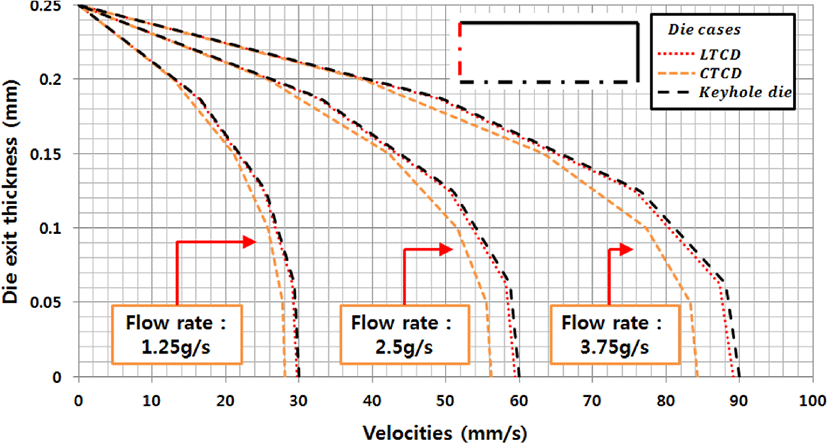
Figure 18에서는 출구의 다이 폭방향으로의 속도 분포를 3 개의 다른 질량유량에 대해 한 그래프에 나타나 있다. 일정한 유량에 대해 속도분포는 1차원 모델로 가정하면 모두 동일하 여야 하나 출구 단면에서 속도분포가 모두 다르므로 중심 단 면에서 속도분포도 다르게 나옴을 볼 수 있다. 모두가 동일하 게 다이 출구 두께 방향으로 Pa rabolic한 형태를 나타내지만 CTCD의 경우 속도가 가장 작게 나오며 그 다음으로 LTCD, Keyhole die순으로 속도 분포를 보이고 있다. 이렇게 출구의 속도 편차가 존재하면 제품의 불량으로 이어지기 때문에 다 이 형상의 최적화가 필요하다.
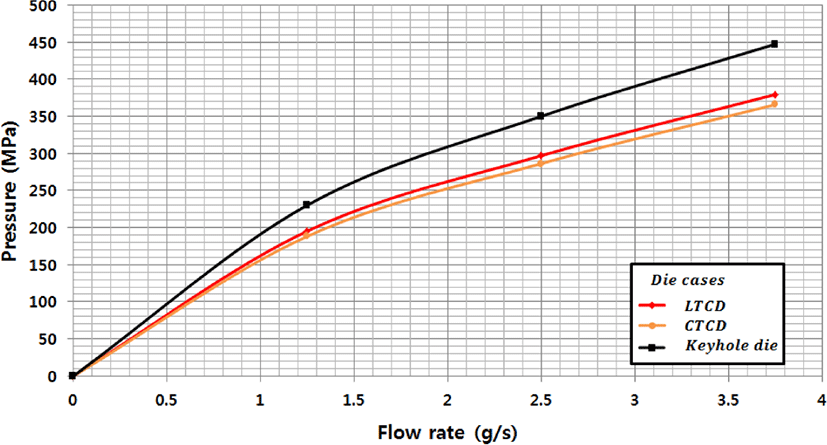
Figure 19에서는 1/4형상 기준으로 각각 1.25(g/s), 2.5(g/s), 3.75(g/s) 유량에 대한 압력 강하를 3가지 다이에서 나타낸 다 이 특성 곡선이다. 동일한 입구 질량유량에 대하여 Keyhole die, LTCD, CTCD순으로 압력이 높아지는 것을 확인하였으 며, Key hole die의 경우 입구에서 First manifold의 폭 방향으 로 끝까지 유동이 진행하기 어려워 다른 2개의 다이 보다 높 은 압력을 보인다. 또한 LTCD와 CTCD의 경우 두 다이의 형 태가 비슷하기 때문에 다이 특성이 유사한 경향을 나타낸다. 이는 다이의 형태가 다른 경우에 재료투입량을 조절하지 못 하면 다이가 변형, 파손되는 경우가 발생할 수 있다는 것을 확 인 할 수 있다.
파워모델지수의 영향을 알아보기 위해 LTCD 다이를 선택하고 질량유량은 1.25(g/s)로 고정하고 파워모델지수를 1, 0.8, 0.6으로 변화시켜 얻은 결과가 Figure 20, 21에 나타내었다. Figure 20과 21은 각각, 파워모델지수 변화에 따른 다이 출구의 속도분포를 폭 방향과 두께 방향으로 하나의 그래프에 그려낸 것이다. 파워모델지수가 1인 경우를 Newtonian이라고 표시하였다. Figure 20, 21에서 알 수 있듯이, 두 경우 모두 파워모델지수가 감소하면서 전단변형률속도의 증가에 따라 점도가 감소하는 전단담화 현상으로 인하여 다이 출구에서 완곡한 프로파일을 형성하게 된다. 1/4형상 기준으로 입구 단면 적 19.63 mm2, 출구 단면적 50 mm2으로 입구 단면적과 출구 단면적의 비율이 0.3926이 되며 입구의 평균 속도가 53.95 mm/s일 때, 출구의 평균 속도는 21.18 mm/s가 되어야 하지만 Figure 20, 21에서 속도 분포는 30 mm/s를 나타내고 있다. 이는 각 부분의 중앙 지점에서 측정한 결과이므로 속도가 더 높게 나올 수 밖에 없으며 다이 출구의 전체 평균 속도를 측정 하면 21.18 mm/s가 된다. Figure 20에서의 폭 방향의 속도 분 포의 경우 Newtonian은 일정한 속도로 토출되며 벽면에서의 속도는 0이 된다. 파워모델지수 값이 감소할수록 Shear thinning 현상으로 인하여 점도가 떨어지고 더 parabolic한 형태를 띄게 되어 출구에서의 속도분포가 균일하지 않게 된다. Figure 21의 두께 방향의 경우에는 파워모델지수 값이 감소하 면서 Shear thinning현상이 발생하고 그 결과 파워모델지수 값이 높은 유체에 비해 더 완곡한 속도 분포가 형성된다.
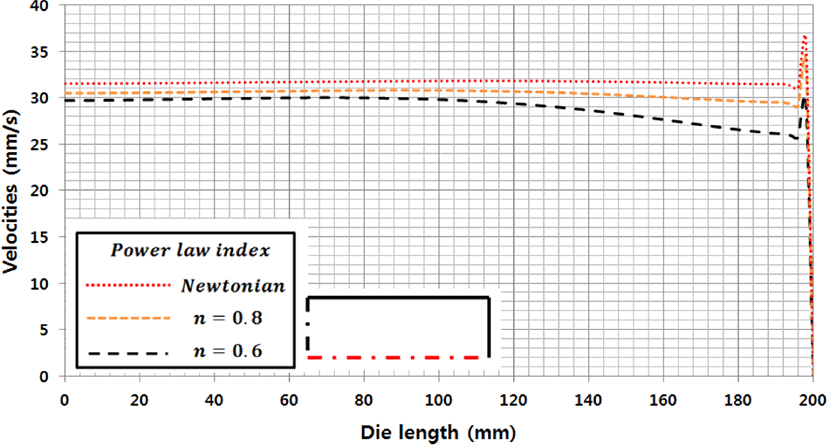
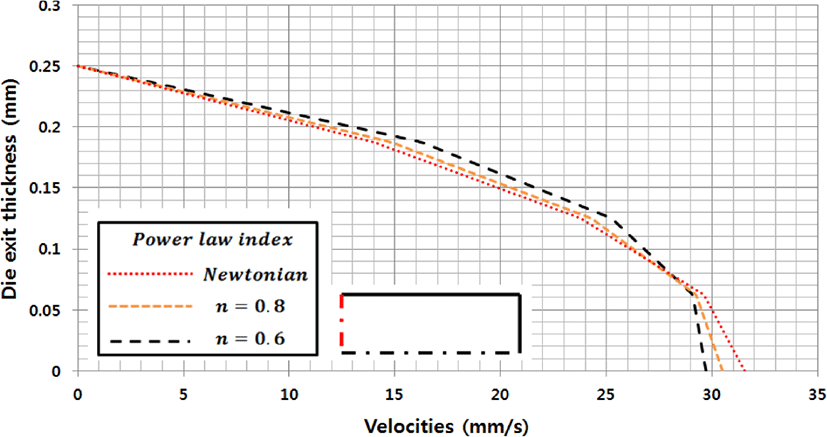
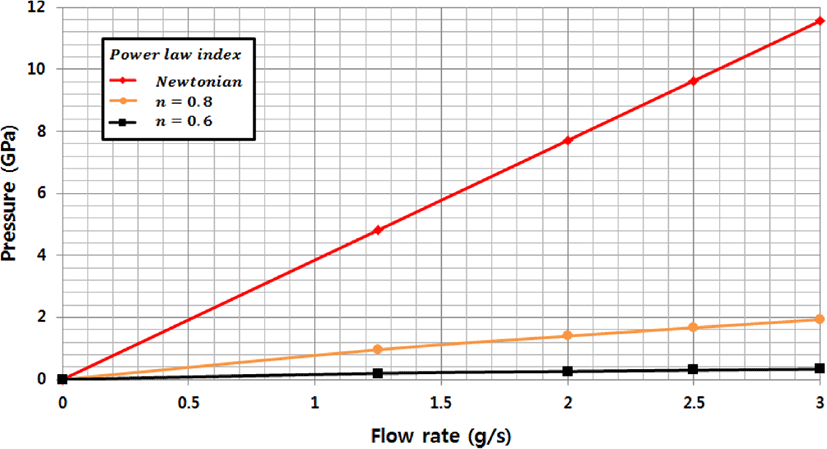
Figure 22는 파워모델지수 변화에 따른 LTCD의 다이특선 곡선이다. 유량은 1.25, 2, 2.5, 3(g/s)로 주어 해석을 진행하였다. 파워모델지수가 1일때 즉, 점도가 일정한 Newtonian 유체는 점도가 일정하므로 다이 특성 곡선이 선형적인 직선의 형태를 띄게 된다. 그러나 Power law index의 값이 작아짐에 따라 다이 특성 곡선은 선형적인 직선의 형태가 아닌 곡선의 형태를 띄게 되는데 이는 다이 내부에서의 Shear rate에 대하여 점도의 감소 비율이 파워모델지수가 작아짐에 따라 더욱 크게 감소하기 때문에, n이 작아지면서 같은 압력하에서 유량 이 커지게 되는데, n값이 작아지면서 Shear thinning현상으로 인하여 점도가 감소하고 그로 인해 높은 점도에서보다 낮은 점도에서 더 많은 토출량이 나오게 된다. 본 연구는 등온으로 해석이 진행되었지만 온도 조건이 합쳐질 경우 다이 셋팅온도가 커질 경우, 더 큰 전단담화 현상이 일어나게 되며 다이 내 압력이 현저히 떨어지게 될 것으로 예상된다.
Conclusions
본 연구에서는 압출 공정에서 여러가지 종류의 다이를 사용하여 다이 특성분석을 위하여 전산 수치해석을 수행하였다. 우선 필름압출공정에서 주로 사용되는 일반적인 T-die를 사용 하여 형상 축소하여 스케일 효과를 관찰하였다. 다이 특성에 서는 일반적인 T-die에 대하여 다이 형상 스케일 모형을 만들 고, 유량에 변화를 주어 다이 특성을 해석하였다. 형상 스케 일에 관계없이, 다이 내부의 압력 및 속도는 입구에서 높았으며 First manifold를 거치며 안정화에 들어가게 되고 Secondary manifold에서 완전한 안정화가 이루어지게 되고 출구까지 길 이방향으로 균일하게 나오게 됨을 확인하였다. 실제 스케일 (big scale) T-die의 특성곡선을 축소 형상(small scale) 모델의 다이특성과 함께 조사한 결과 축소된 모델의 압력 증가 현상 으로 두 모델의 다이특성의 차이를 뚜렷하게 나타났다. scale-down과 scale-up 다이에서의 속도 분포에 대하여는 재료의 유변학적 특성에 의존하지만 Figure 10, 17, 20을 비교하여 보면 scale-up 하였을 경우 속도 분포 격차가 커진다. 이로부터 압력분포도 균일하지 않게 되며 유선 모양도 다이 출구에서 균일 유동에서 멀어질 것이라 예상된다.
3가지 서로 다른 다이에 대하여 다이 출구에서의 속도 분포는 폭 방향으로 LTCD, Keyhile die의 경우에는 Parabolic한 형태를 나타내지만 LTCD의 경우 역으로 중앙부분의 속도가 낮게 나타난다. 또한 각각의 다이 특성은 동일한 유량에 대하여 Keyhole die, LTCD, CTCD순으로 압력이 높아지는 것을 확인하였다. 모두가 동일하게 다이 출구 두께 방향으로 Parabolic한 형태를 나타내지만 CTCD의 경우 속도가 가장 작 게 나오며 그 다음으로 LTCD, Keyhole die순으로 속도 분포를 보이고 있다. 이렇게 출구의 속도 편차가 존재하면 제품의 불량으로 이어지기 때문에 다이 형상의 최적화가 필요하다.
LTCD 다이에서 파워모델지수 변화에 대하여 관찰한 결과, n값이 작아지면서 전단담화 현상으로 인하여 점도가 감소하고 그로 인해 더 많은 토출량이 나오게 됨을 특성 곡선으로부터 이해 할 수 있었다.
향후 다이특성 그래프와 스크류 특성 그래프를 하나의 그 래프에 나타내어 공정조건를 찾아내고 이에 대한 데이터 베이스를 제시하고 각각의 다이 및 스크류, 재료에 대하여 데이터 베이스를 쌓는다면 이 후 여러 공정 조건에 대하여 스크류-다이 특성 곡선 경향성을 분석하여 실험 없이 가공공정에 대한 최적조건을 찾을 수 있을 것으로 기대된다.