Development of Hyperelastic Model for Butadiene Rubber Using a Neural Network

In the following, the mechanics of rubber material are briefly revised. The local gradient of deformation is denoted $\underset{\_}{\underset{\_}{F}}$. The right Cauchy-Green deformation tensor is then related to $\underset{\_}{\underset{\_}{F}}$ by:

The strain invariants, denoted I₁, I₂, I₃ , are given by:

Hyperelastic materials normally experience large deformation in many applications. Due to large strain problems, two major stress tensors are considered and defined, the true stress tensor s and the first Piola-Kirchoff (also called the nominal) stress tensor $\underset{\_}{\underset{\_}{P}}$. These physical quantities are related by:

In this study, our investigated material is assumed to be homogeneous, isotropic, rate-independent, and incompressible. Therefore, the kinematic condition must be satisfied, which is represented by: $J=\det \left(\underset{\_}{\underset{\_}{F}}\right)=I_3=1$. The first Piola-Kirchoff stress tensor can be rewritten:

where ρ is the Lagrange multiplier associated with the incompressibility constraint.

For further details, readers are encouraged to refer for example to.⁷

In this section, we shortly discuss the formulations of widely used hyperelastic models for rubber-like materials.

Neo-Hookean model is one of the simple models for incompressible materials where the strain density function is a linear function of only the first strain invariant as follows:

A Mooney-Rivlin model is introduced by Melvin Mooney and Ronald Rivlin, where the strain energy density function is a linear combination of two strain invariants:⁸

An Ogden model is a different approach to those two above models.⁹

This model expresses the strain energy density function in terms of principal stretch ratios. For example, the third-order Ogden model has that function defined by:

In this study, the neural network-based hyperelastic model is investigated to reproduce theoretically the stress-strain curves obtained from uniaxial and equibiaxial tension of industrial rubber used in automotive engine bush. The input of this model is deformation gradient $\underset{\_}{\underset{\_}{F}}$ (in the shape of 3×3), and the output is nominal stress tensor $\underset{\_}{\underset{\_}{P}}$ (also in the shape of 3×3). The structure of the model is demonstrated in Figure 1.

Figure 1. Structure of the neural network (red arrow denotes trainable weights between two dense layers).

Download Original Figure

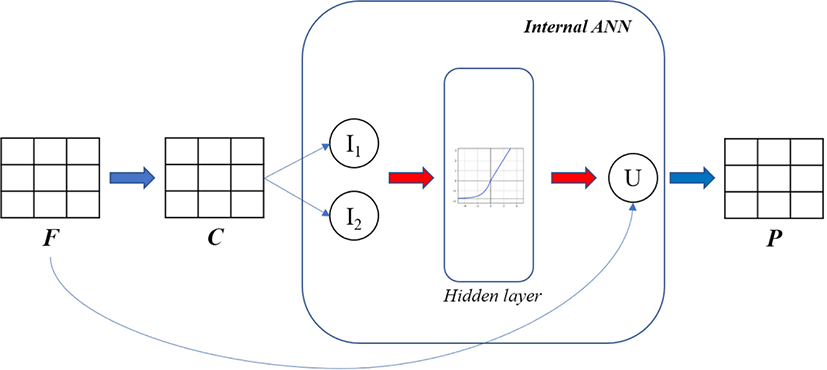
Conventional models for incompressible rubber-like materials such as Ogden, Neo-Hookean, Mooney-Rivlin, define strain energy density (denoted U) explicitly as an expression of stretch ratios or strain invariants. In the proposed method of this study, this relationship is undecided and left open to learning from data using an internal ANN with one hidden layer and a Scaled Exponential Linear Unit (SELU) activation function.¹⁰

This internal ANN accepts two strain invariants as input and results in a scalar value of strain density potential, as shown in Figure 1.

The hyperparameters in the model include the number of hidden units, learning rate, the initialization methods, the number of epochs, and batch size.

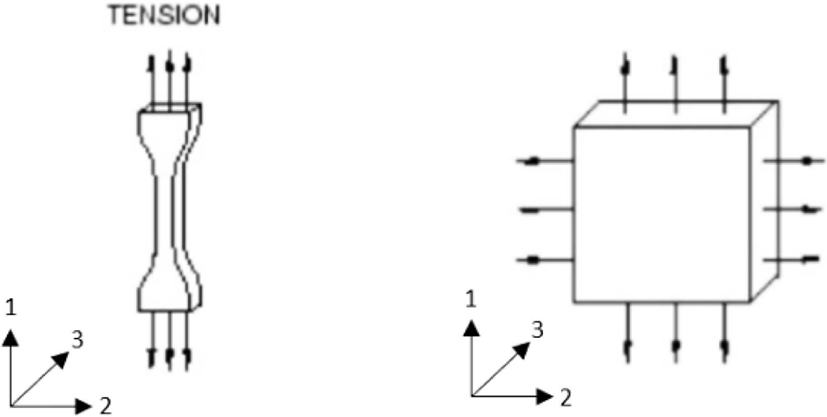
Two testing modes are conducted to obtain stress and strain data, as demonstrated in Figure 2 with a fixed coordinate system. These experimental data are then processed into the inputs and outputs of the model. The details are discussed in the next section. It is important to note that the rubber specimen should be stabilized by stretching several times to reach two or three maximum strain levels beforehand.¹¹

Figure 2. Illustration of testing methods.

Download Original Figure

The model is implemented in the Python-based machine learning library Keras-Tensorflow, using symbol-to-symbol automatic differentiation in the library.¹²

The raw data from experiments are processed to get the stable stress-strain curves in uniaxial and biaxial modes. Thus, the test set of deformation gradient inputs and engineering stress tensor outputs is obtained. Afterward, they are applied to the training process. The number of hidden units in the hidden layer is varied to have reasonable curve fitting compared to experiments, depending on the complexity of the multi-axial stress-strain relationship of the material. In this rubber material, we found that 6-8 units in the hidden layers result in a satisfactory fitting. The training algorithm is Adam with default parameters. The hyperparameters of the model are shown in Table 1.

In this work, we compared the neural network-based model with three widely used conventional hyperelastic models: Ogden 3^rd, Neo-Hookean, Mooney-Rivlin. The material constants for these models are obtained from ABAQUS.

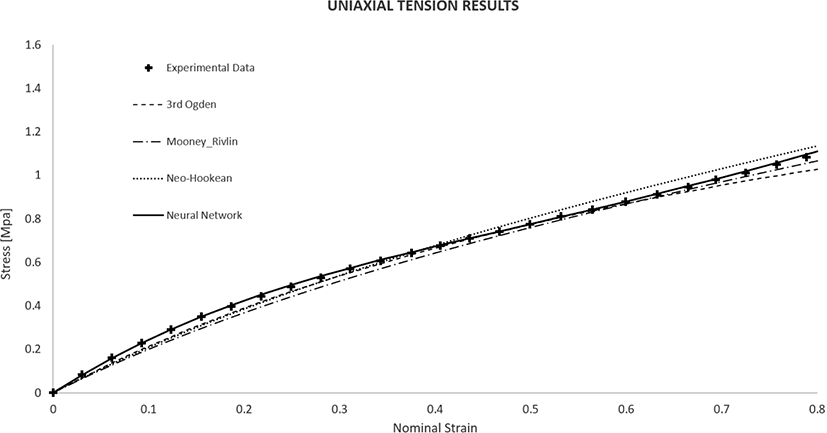
Figure 3 shows the results of hyperelastic models for the uniaxial tension test. As shown in Figure 3, the neural network model has better agreement with experiments than the conventional models do. Ogden 3^rd model fits accurately up to a strain level of about 20%. In addition, Mooney-Rivlin and Neo-Hookean models match the data in a strain range of 30%-60%.

Figure 3. Equibiaxial extension test results.

Download Original Figure

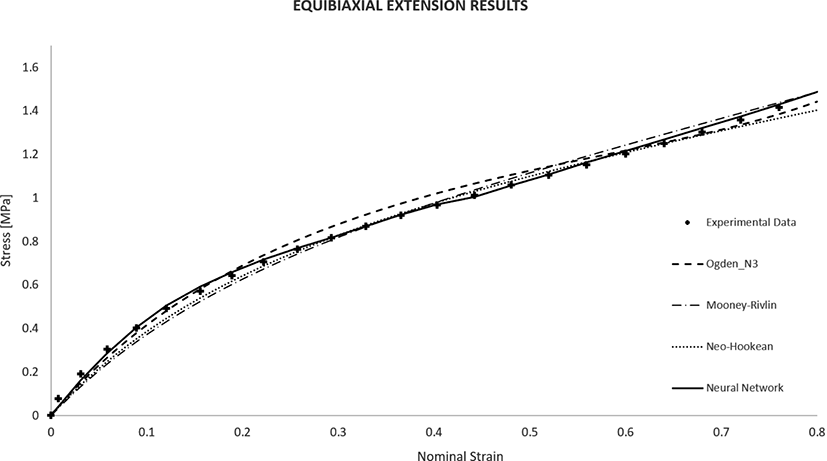
The results for the uniaxial test are shown in Figure 4. The neural network model fits the experiments efficiently. For a low strain range below 40%, conventional models are not enough to represent the non-linearity of the material. Ogden 3^rd model and Mooney-Rivlin model match the data in a moderate strain range of 45%-65%.

Figure 4. Uniaxial tension test results.

Download Original Figure

To verify the implementation of the proposed hyperelastic model using a neural network in a commercial FEA software, the UHYPER subroutine of ABAQUS was coded based on the fully trained model. The analysis of the biaxial extension test is reproduced, and Figure 5 shows the strain distribution.

Figure 5. Analysis results of equibiaxial tension test. (a) Undeformed body, (b) Strain distribution of deformed body

Download Original Figure